题目内容
10.已知向量$\overrightarrow a=(cosx-sinx,\sqrt{2})$,$\overrightarrow b=(cosx+sinx,-\sqrt{2})(x∈R)$,则函数$f(x)=\overrightarrow a•\overrightarrow b$是( )| A. | 周期为π的偶函数 | B. | 周期为π的奇函数 | ||
| C. | 周期为$\frac{π}{2}$的偶函数 | D. | 周期为$\frac{π}{2}$的奇函数 |
分析 利用数量积公式和二倍角公式化简f(x).
解答 解:$f(x)=\overrightarrow a•\overrightarrow b$=(cosx-sinx)(cosx+sinx)-2=cos2x-sin2x-2=cos2x-2.
∴f(x)的周期为π.
∵f(-x)=cos(-2x)-2=cos2x-2=f(x),
∴f(x)是偶函数.
故选A.
点评 本题考查了平面向量的数量积运算,三角函数的恒等变换,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.已知点A(1,2,-1),点C与点A关于平面xOy对称,点B与点A关于x轴对称,则线段BC的长为( )
| A. | 2$\sqrt{2}$ | B. | 4 | C. | 2$\sqrt{5}$ | D. | 2$\sqrt{7}$ |
5.如图,在△ABC中,AD⊥AB,$\overrightarrow{BC}=2\sqrt{3}\overrightarrow{BD}$,$|{\overrightarrow{AD}}|=1$,则$\overrightarrow{AC}•\overrightarrow{AD}$=( )
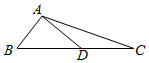

| A. | $2\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
15.有5个大小、质地都相同的小球,标号分别为1,3,5,7,9,从中任取三个小球,其标号之和能够被3整除的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{1}{2}$ |
2.函数y=x2cosx在x=1处的导数是( )
| A. | 0 | B. | 2cos1-sin1 | C. | cos1-sin1 | D. | 1 |
19.两圆x2+y2=9和x2+y2-18x+16y+45=0的公切线有( )条.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
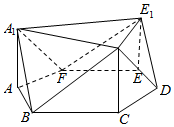 已知如图几何体A1C1E1-ABCDEF底面是边长为2的六变形,AA1,CC1,EE1长度为2且都垂直与底面,
已知如图几何体A1C1E1-ABCDEF底面是边长为2的六变形,AA1,CC1,EE1长度为2且都垂直与底面,