题目内容
5.如图,在△ABC中,AD⊥AB,$\overrightarrow{BC}=2\sqrt{3}\overrightarrow{BD}$,$|{\overrightarrow{AD}}|=1$,则$\overrightarrow{AC}•\overrightarrow{AD}$=( )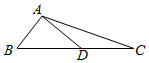
| A. | $2\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
分析 用$\overrightarrow{AB},\overrightarrow{AD}$表示$\overrightarrow{AC}$,再计算数量积.
解答 解:∵AD⊥AB,∴$\overrightarrow{AB}•\overrightarrow{AD}$=0.
∵$\overrightarrow{AC}$=2$\sqrt{3}$$\overrightarrow{BD}$=2$\sqrt{3}$($\overrightarrow{AD}-\overrightarrow{AB}$)=2$\sqrt{3}$$\overrightarrow{AD}$-2$\sqrt{3}$$\overrightarrow{AB}$.
∴$\overrightarrow{AC}•\overrightarrow{AD}$=(2$\sqrt{3}$$\overrightarrow{AD}$-2$\sqrt{3}$$\overrightarrow{AB}$)•$\overrightarrow{AD}$=2$\sqrt{3}$$\overrightarrow{AD}$2-2$\sqrt{3}$$\overrightarrow{AB}•\overrightarrow{AD}$=2$\sqrt{3}$.
故选:A.
点评 本题考查了平面向量的数量积运算,属于基础题.

练习册系列答案
相关题目
15.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{25}$=1(a>5)的两个焦点为F1、F2,且|F1F2|=8.弦AB过点F1,则△ABF2的周长为( )
| A. | 10 | B. | 20 | C. | 2$\sqrt{41}$ | D. | 4$\sqrt{41}$ |
10.已知向量$\overrightarrow a=(cosx-sinx,\sqrt{2})$,$\overrightarrow b=(cosx+sinx,-\sqrt{2})(x∈R)$,则函数$f(x)=\overrightarrow a•\overrightarrow b$是( )
| A. | 周期为π的偶函数 | B. | 周期为π的奇函数 | ||
| C. | 周期为$\frac{π}{2}$的偶函数 | D. | 周期为$\frac{π}{2}$的奇函数 |
17.在正方体ABCD-A1B1C1D1中,点E,F分别是棱AB,BB1的中点,则异面直线EF和BC1所成的角是( )
| A. | 60° | B. | 45° | C. | 90° | D. | 120° |
14.某几何体的三视图如图所示,则其体积为( )


| A. | 4 | B. | $4\sqrt{2}$ | C. | $4\sqrt{3}$ | D. | 8 |
15.椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的两焦点为F1(-c,0)、F2(c,0),P为直线$x=\frac{a^2}{c}$上一点,F1P的垂直平分线恰过F2点,则e的取值范围为( )
| A. | $({0,\frac{{\sqrt{3}}}{3}})$ | B. | $({0,\frac{{\sqrt{3}}}{3}}]$ | C. | $({\frac{{\sqrt{3}}}{3},1})$ | D. | $[{\frac{{\sqrt{3}}}{3},1})$ |