题目内容
19．两圆x2+y2=9和x2+y2-18x+16y+45=0的公切线有（ ）条．| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 把两圆的方程化为标准形式，求出圆心和半径，根据两圆的圆心距小于半径之和，可得两圆相交，由此可得两圆的公切线的条数．
解答 解：圆x2+y2=9表示以（0，0）为圆心，半径等于3的圆．
圆x2+y2-18x+16y+45=0，即（x-9）2+（y+8）2=100，表示以（9，-8）为圆心，半径等于10的圆．
两圆的圆心距等于$\sqrt{81+64}$=$\sqrt{145}$，小于半径之和，大于半径差，故两圆相交，故两圆的公切线的条数为2，
故选B．
点评 本题主要考查圆的标准方程的特征，两圆的位置关系的确定方法，属于中档题．
练习册系列答案
每课必练系列答案
相关题目
10．已知向量$\overrightarrow a=（cosx-sinx，\sqrt{2}）$，$\overrightarrow b=（cosx+sinx，-\sqrt{2}）（x∈R）$，则函数$f（x）=\overrightarrow a•\overrightarrow b$是（ ）
| A． | 周期为π的偶函数 | B． | 周期为π的奇函数 | ||
| C． | 周期为$\frac{π}{2}$的偶函数 | D． | 周期为$\frac{π}{2}$的奇函数 |
7．已知A（-1，2，1），B（1，3，4），则（ ）
| A． | $\overrightarrow{AB}$=（-1，2，1） | B． | $\overrightarrow{AB}$=（1，3，4） | C． | $\overrightarrow{AB}$=（2，1，3） | D． | $\overrightarrow{AB}$=（-2，-1，-3） |
14．某几何体的三视图如图所示，则其体积为（ ）
| A． | 4 | B． | $4\sqrt{2}$ | C． | $4\sqrt{3}$ | D． | 8 |
4．
根据如图程序框图，当输入5时，输出的是（ ）
根据如图程序框图，当输入5时，输出的是（ ）| A． | 6 | B． | 4.6 | C． | 1.9 | D． | -3.9 |
如图，正方体AC1的棱长为1，过点A作平面A1BD的垂线，垂足为点H，以下四个命题：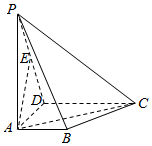
如图，ABCD是梯形，AB∥CD，∠BAD=90°，PA⊥面ABCD，且AB=1，AD=1，CD=2，PA=3，E为PD的中点．