题目内容
15.有5个大小、质地都相同的小球,标号分别为1,3,5,7,9,从中任取三个小球,其标号之和能够被3整除的概率是( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{1}{2}$ |
分析 先求出基本事件总数,再求出任取三个小球,其标号之和能够被3整除,包含的基本事件个数,由此能求出从中任取三个小球,其标号之和能够被3整除的概率.
解答 解:5个大小、质地都相同的小球,标号分别为1,3,5,7,9,从中任取三个小球,
基本事件总数n=${C}_{5}^{3}$=10,
任取三个小球,其标号之和能够被3整除,包含的基本事件有:
{1,3,5},{3,5,7},{1,5,9},{5,7,9},共4个,
∴从中任取三个小球,其标号之和能够被3整除的概率p=$\frac{4}{10}$=$\frac{2}{5}$.
故选:B.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
相关题目
10.已知向量$\overrightarrow a=(cosx-sinx,\sqrt{2})$,$\overrightarrow b=(cosx+sinx,-\sqrt{2})(x∈R)$,则函数$f(x)=\overrightarrow a•\overrightarrow b$是( )
| A. | 周期为π的偶函数 | B. | 周期为π的奇函数 | ||
| C. | 周期为$\frac{π}{2}$的偶函数 | D. | 周期为$\frac{π}{2}$的奇函数 |
7.已知A(-1,2,1),B(1,3,4),则( )
| A. | $\overrightarrow{AB}$=(-1,2,1) | B. | $\overrightarrow{AB}$=(1,3,4) | C. | $\overrightarrow{AB}$=(2,1,3) | D. | $\overrightarrow{AB}$=(-2,-1,-3) |
4. 根据如图程序框图,当输入5时,输出的是( )
根据如图程序框图,当输入5时,输出的是( )
 根据如图程序框图,当输入5时,输出的是( )
根据如图程序框图,当输入5时,输出的是( )| A. | 6 | B. | 4.6 | C. | 1.9 | D. | -3.9 |
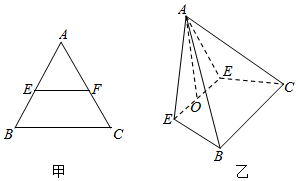 如图甲,在边长为4的等边△ABC中,点E,F分别为AB,AC上一点,且EF∥BC,EF=2a,沿EF将△AEF折起,使得平面AEF⊥平面EFCB,形成一个如图乙所示的四棱锥,设O为EF的中点.
如图甲,在边长为4的等边△ABC中,点E,F分别为AB,AC上一点,且EF∥BC,EF=2a,沿EF将△AEF折起,使得平面AEF⊥平面EFCB,形成一个如图乙所示的四棱锥,设O为EF的中点.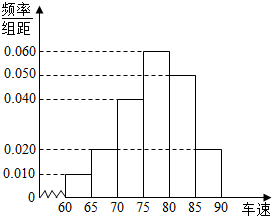 2014年“双节”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90)后得到如图的频率分布直方图.
2014年“双节”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90)后得到如图的频率分布直方图.