题目内容
已知等差数列{an}，首项a1=1，公差d=3，若an=2014，则n等于（ ）
| A、670 | B、671 |
| C、672 | D、673 |
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：利用等差数列的通项公式即可得出．
解答：
解：∵首项a1=1，公差d=3，an=2014，
∴2014=1+3（n-1），解得n=672．
故选：C．
∴2014=1+3（n-1），解得n=672．
故选：C．
点评：本题考查了等差数列的通项公式，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
在集合M={1，2，3，4}的所有非空子集中，任取一个集合，恰好满足条件“?x∈A，则6-x∈A”的集合的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
下列四个命题中，真命题的是（ ）
| A、2是偶数且是无理数 |
| B、有些梯形内接于圆 |
| C、空间中的两个向量可能不共面 |
| D、?x∈R，x2-x-1≠0 |
已知圆C的内接正三角形的边长为
，且圆心为直线x-y+1=0与x轴的交点，则圆C的方程为（ ）
| 3 |
| A、（x-1）2+y2=1 |
| B、（x-1）2+y2=4 |
| C、（x+1）2+y2=1 |
| D、（x+1）2+y2=4 |
已知等差数列{an}中，a2+a8=2，a5+a11=8，则其公差是（ ）
| A、6 | B、3 | C、2 | D、1 |
设集合A={y|y=2x，x∈R}，B={y|y=x2，x∈R}，则下列结论正确的是（ ）
| A、A?B |
| B、B?A |
| C、A∩B={（2，4）} |
| D、A∩B={2，4} |
某城市有3个演习点同时进行消防演习，现将4个消防队分配到这3个演习点，若每个演习点至少安排1个消防队，则不同的分配方案种数位（ ）
| A、12 | B、36 | C、72 | D、108 |
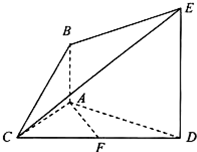如图，已知AB⊥平面ACD，DE∥AB，△ACD是正三角形，AD=4，DE=2AB=3，且F是CD的中点．