题目内容
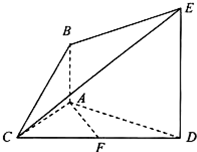 如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=4,DE=2AB=3,且F是CD的中点.
如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=4,DE=2AB=3,且F是CD的中点.(1)求证:AF∥平面BCE;
(2)在线段CE上是否存在点H,使DH⊥平面BCE?若存在,求出
| CH |
| HE |
考点:直线与平面平行的性质,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)易证四边形ABGF是平行四边形,从而得到AF∥平面BCE;
(2)存在,过D在平面CDE内作DH⊥CE,垂足为H,则点H即为所求,易证平面BCE⊥平面CDE,在在Rt△CDE中,DE=3,CD=4,CE=5,由射影定理,CH=
,HE=
,问题得以解决.
(2)存在,过D在平面CDE内作DH⊥CE,垂足为H,则点H即为所求,易证平面BCE⊥平面CDE,在在Rt△CDE中,DE=3,CD=4,CE=5,由射影定理,CH=
| 16 |
| 5 |
| 9 |
| 5 |
解答:
解:(1)取CE的中点G,连FG,BG,
QF为CD之中点,∴GF∥
DE,
又由已知AB∥
DE,
∴GF∥AB且GF=AB,
四边形ABGF是平行四边形,
∴BG∥AF,
AF?平面BCE,BG?平面BCE,
∴AF∥平面BCE,
(2)△ACD为正三角形,且F是CD的中点.
∴AF⊥CD,又AB⊥平面ACD,DE∥AB,平面ACD,而AF?平面ACD,
∴AF⊥DE,又DE∩CD=D,
∴AF⊥平面CDE
在(1)中BG∥AF,
∴BG⊥平面CDE,而BG?平面BCE,
∴平面BCE⊥平面CDE,
且平面BCE∩平面CDE=CE,而DH⊥CE.DH?平面CDE,
∴DH⊥平面BCE,
在Rt△CDE中,DE=3,CD=4,
∴CE=5,
由射影定理,CH=
,HE=
,
∴
=
.
QF为CD之中点,∴GF∥
| 1 |
| 2 |
又由已知AB∥
| 1 |
| 2 |
∴GF∥AB且GF=AB,
四边形ABGF是平行四边形,
∴BG∥AF,
AF?平面BCE,BG?平面BCE,
∴AF∥平面BCE,
(2)△ACD为正三角形,且F是CD的中点.

∴AF⊥CD,又AB⊥平面ACD,DE∥AB,平面ACD,而AF?平面ACD,
∴AF⊥DE,又DE∩CD=D,
∴AF⊥平面CDE
在(1)中BG∥AF,
∴BG⊥平面CDE,而BG?平面BCE,
∴平面BCE⊥平面CDE,
且平面BCE∩平面CDE=CE,而DH⊥CE.DH?平面CDE,
∴DH⊥平面BCE,
在Rt△CDE中,DE=3,CD=4,
∴CE=5,
由射影定理,CH=
| 16 |
| 5 |
| 9 |
| 5 |
∴
| CH |
| HE |
| 16 |
| 9 |
点评:本题主要考查了线面平行的判定定理和面面垂直的判定定理以及射影定理,属于中档题.

练习册系列答案
相关题目
已知等差数列{an},首项a1=1,公差d=3,若an=2014,则n等于( )
| A、670 | B、671 |
| C、672 | D、673 |
定义
?
=
,若
=(1,2),
=(3,-2),则与
?
反向的向量为( )
| a |
| b |
| ||||
|
| a |
| b |
| a |
| b |
| A、(5,-6) |
| B、(5,6) |
| C、(-5,6) |
| D、(-5,-6) |
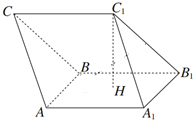 如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心,AA1=2
如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心,AA1=2 如图,在Rt△ABC中,AB=BC,以AB为直径的⊙O交AC于D,过D作DE⊥BC,垂足为E,连接AE交⊙O于点F,求证:CE2=EF•EA.
如图,在Rt△ABC中,AB=BC,以AB为直径的⊙O交AC于D,过D作DE⊥BC,垂足为E,连接AE交⊙O于点F,求证:CE2=EF•EA.