题目内容
已知圆C的内接正三角形的边长为
,且圆心为直线x-y+1=0与x轴的交点,则圆C的方程为( )
| 3 |
| A、(x-1)2+y2=1 |
| B、(x-1)2+y2=4 |
| C、(x+1)2+y2=1 |
| D、(x+1)2+y2=4 |
考点:圆的标准方程
专题:直线与圆
分析:由条阿金利用正弦定理求得半径R的值,再根据圆心为直线x-y+1=0与x轴的交点,求出圆心的坐标,可得圆C的方程.
解答:
解:设圆C的半径为R,由正弦定理可得
=2R,R=1.
再根据直线x-y+1=0与x轴的交点为(-1,0),
故圆C的方程为(x+1)2+y2=1,
故选:C.
| ||
| sin60° |
再根据直线x-y+1=0与x轴的交点为(-1,0),
故圆C的方程为(x+1)2+y2=1,
故选:C.
点评:本题主要考查求圆的标准方程的方法,正弦定理的应用,属于基础题.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
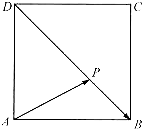 如图,点P为正方形ABCD对角线BD上的点,若
如图,点P为正方形ABCD对角线BD上的点,若| AP |
| PB |
A、4
| ||
| B、4 | ||
C、2
| ||
| D、2 |
等差数列{an}中,a1=1,a3=4,则公差d等于( )
| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
已知tanx=5,则
=( )
| sinx+3cosx |
| sinx-cosx |
| A、1 | B、2 | C、3 | D、4 |
已知等差数列{an},首项a1=1,公差d=3,若an=2014,则n等于( )
| A、670 | B、671 |
| C、672 | D、673 |
已知抛物线的焦点坐标是(0,
),则它的标准方程是( )
| 1 |
| 2 |
| A、y2=x |
| B、x2=2y |
| C、x2=y |
| D、y2=2x |
直线y=-x+1的倾斜角为( )
| A、30° | B、45° |
| C、135° | D、150° |