题目内容
设集合A={y|y=2x,x∈R},B={y|y=x2,x∈R},则下列结论正确的是( )
| A、A?B |
| B、B?A |
| C、A∩B={(2,4)} |
| D、A∩B={2,4} |
考点:集合的包含关系判断及应用
专题:集合
分析:?x∈R,可得2x>0,x2≥0.即可得出A,B的关系.
解答:
解:?x∈R,可得2x>0,x2≥0.
∴A=(0,+∞),B=[0,+∞).
∴A?B.
故选:A.
∴A=(0,+∞),B=[0,+∞).
∴A?B.
故选:A.
点评:本题考查了指数函数、二次函数的单调性、集合之间的关系,属于基础题.

练习册系列答案
相关题目
等差数列{an}中,a1=1,a3=4,则公差d等于( )
| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
已知等差数列{an},首项a1=1,公差d=3,若an=2014,则n等于( )
| A、670 | B、671 |
| C、672 | D、673 |
已知抛物线的焦点坐标是(0,
),则它的标准方程是( )
| 1 |
| 2 |
| A、y2=x |
| B、x2=2y |
| C、x2=y |
| D、y2=2x |
直线y=-x+1的倾斜角为( )
| A、30° | B、45° |
| C、135° | D、150° |
定义
?
=
,若
=(1,2),
=(3,-2),则与
?
反向的向量为( )
| a |
| b |
| ||||
|
| a |
| b |
| a |
| b |
| A、(5,-6) |
| B、(5,6) |
| C、(-5,6) |
| D、(-5,-6) |
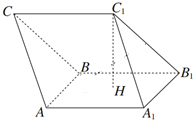 如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心,AA1=2
如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心,AA1=2