题目内容
8．已知i为虚数单位，复数$z=\frac{1+2i}{i-1}$，则复数z的虚部是（ ）| A． | $-\frac{3}{2}i$ | B． | $-\frac{3}{2}$ | C． | $\frac{3}{2}i$ | D． | $\frac{3}{2}$ |
分析 直接利用复数代数形式的乘除运算化简得答案．
解答 解：$z=\frac{1+2i}{i-1}$=$\frac{（1+2i）（-1-i）}{（-1-i）（-1+i）}$=$\frac{1-3i}{2}$=$\frac{1}{2}$-$\frac{3}{2}$i，
∴复数z的虚部为-$\frac{3}{2}$．
故选：B
点评 本题考查了复数代数形式的乘除运算，考查了复数的基本概念，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
15．已知等比数列{an}的前n项和为Sn，若S3=7，S6=63，则数列{nan}的前n项和为（ ）
| A． | -3+（n+1）×2n | B． | 3+（n+1）×2n | C． | 1+（n+1）×2n | D． | 1+（n-1）×2n |
19．已知f（x）是定义在实数集R上的不恒为零的偶函数，且xf（x+1）=（x+1）f（x）对任意实数x恒成立，则$f[f（\frac{5}{2}）]$的值是（ ）
| A． | 0 | B． | $\frac{1}{2}$ | C． | 1 | D． | $\frac{5}{2}$ |
16．若定义运算a*b为：a*b=$\left\{\begin{array}{l}{a，a≤b}\\{b，a＞b}\end{array}\right.$，如1*2=1，则函数f（x）=2x*2-x的值域为（ ）
| A． | R | B． | （0，1] | C． | （0，+∞） | D． | [1，+∞） |
3．设椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点为F，椭圆C上的两点A，B关于原点对称，且满足$\overrightarrow{FA}$•$\overrightarrow{FB}$=0，若|FA|=|FB|，则椭圆C的离心率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\sqrt{3}-1$ | D． | $\frac{\sqrt{3}}{2}$ |
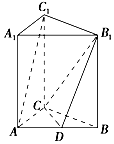如图，三棱柱ABC-A1B1C1的侧棱与底面垂直，AC=9，BC=12，AB=15，AA1=12，点D是AB的中点．