题目内容
20.已知0≤φ<π,函数$f(x)=\frac{{\sqrt{3}}}{2}cos(2x+φ)+{sin^2}x$.(Ⅰ)若$φ=\frac{π}{6}$,求f(x)的单调递增区间;
(Ⅱ)若f(x)的最大值是$\frac{3}{2}$,求φ的值.
分析 (Ⅰ)利用两角和与差的三角函数化简函数的解析式,通过正弦函数的单调性求解即可.
(Ⅱ)利用函数f(x)的最大值为$\frac{3}{2}$,通过求解方程求解即可.
解答 (本小题满分14分)
(Ⅰ)由题意$f(x)=\frac{1}{4}cos2x-\frac{{\sqrt{3}}}{4}sin2x+\frac{1}{2}$…(3分)
=$\frac{1}{2}cos(2x+\frac{π}{3})+\frac{1}{2}$…(5分)
由$2kπ-π≤2x+\frac{π}{3}≤2kπ$,得$kπ-\frac{2π}{3}≤x≤kπ-\frac{π}{6}$.
所以单调f(x)的单调递增区间为$[kπ-\frac{2π}{3},kπ-\frac{π}{6}]$,k∈Z.…(8分)
(Ⅱ)由题意$f(x)=(\frac{{\sqrt{3}}}{2}cosφ-\frac{1}{2})cos2x-\frac{{\sqrt{3}}}{2}sinφsin2x+\frac{1}{2}$,…(10分)
由于函数f(x)的最大值为$\frac{3}{2}$,即${(\frac{{\sqrt{3}}}{2}cosφ-\frac{1}{2})^2}+{(\frac{{\sqrt{3}}}{2}sinφ)^2}=1$,…(12分)
从而cosφ=0,又0≤φ<π,故$φ=\frac{π}{2}$. …(14分)
点评 本题考查两角和与差的三角函数,正弦函数的单调性的应用,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.记数列{an}的前n项和为Sn,若Sn=3an+1,则a10=( )
| A. | -$\frac{{3}^{9}}{{2}^{10}}$ | B. | -$\frac{{3}^{10}}{{2}^{10}}$ | C. | $\frac{{3}^{9}}{{2}^{10}}$ | D. | $\frac{{3}^{10}}{{2}^{10}}$ |
8.已知i为虚数单位,复数$z=\frac{1+2i}{i-1}$,则复数z的虚部是( )
| A. | $-\frac{3}{2}i$ | B. | $-\frac{3}{2}$ | C. | $\frac{3}{2}i$ | D. | $\frac{3}{2}$ |
12.过点M(2,-2p)作抛物线x2=2py(p>0)的两条切线,切点分别为A,B,若线段AB中点的纵坐标为6,则抛物线的方程为( )
| A. | x2=2y | B. | x2=4y | C. | x2=2y或x2=4y | D. | x2=3y或x2=2y |
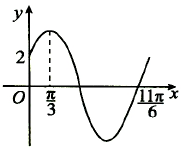 已知函数$f(x)=Asin(ωx+φ)(ω>0,0<φ<\frac{π}{2})$的部分图象如图所示.
已知函数$f(x)=Asin(ωx+φ)(ω>0,0<φ<\frac{π}{2})$的部分图象如图所示.