题目内容
18．设函数$f（x）=2sin（\frac{π}{3}x+\frac{π}{2}）$，若对任意x都有f（x1）≤f（x）≤f（x2），则|x1-x2|的最小值为（ ）| A． | 2 | B． | 4 | C． | 3 | D． | 6 |
分析 利用正弦函数的周期性以及最值，可得|x1-x2|的最小值为$\frac{T}{2}$=$\frac{π}{ω}$，从而求得|x1-x2|的最小值．
解答 解：∵函数$f（x）=2sin（\frac{π}{3}x+\frac{π}{2}）$，若对任意x都有f（x1）≤f（x）≤f（x2），
则|x1-x2|的最小值为$\frac{T}{2}$=$\frac{π}{ω}$=$\frac{π}{\frac{π}{3}}$=3，
故选：C．
点评 本题主要考查正弦函数的周期性以及最值，属于基础题．
练习册系列答案
53随堂测系列答案
相关题目
8．已知i为虚数单位，复数$z=\frac{1+2i}{i-1}$，则复数z的虚部是（ ）
| A． | $-\frac{3}{2}i$ | B． | $-\frac{3}{2}$ | C． | $\frac{3}{2}i$ | D． | $\frac{3}{2}$ |
13．若曲线y=x2+ax+b在点（0，b）处的切线方程是3x-y+1=0，则（ ）
| A． | a=-3，b=1 | B． | a=3，b=1 | C． | a=-3，b=-1 | D． | a=3，b=-1 |
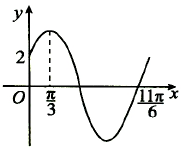已知函数$f（x）=Asin（ωx+φ）（ω＞0，0＜φ＜\frac{π}{2}）$的部分图象如图所示．