题目内容
M=
+
+
+
,当x,y变化时M的最小值为 .
| x2+y2 |
| x2+(y-1)2 |
| (x-1)2+y2 |
| (x-1)2+(y-1)2 |
考点:函数的最值及其几何意义
专题:平面向量及应用
分析:设A(0,0),B(1,0),C(1,1),D(0,1),P(x,y),则M=|PA|+|PD|+|PB|+|PC|=(|AP|+|PC|)+(|BP|+|PD|)=(|
|+|
|)+(|
|+|
|),再用不等式|
|+|
|≥|
+
|求最小值.
| AP |
| PC |
| BP |
| PD |
| a |
| b |
| a |
| b |
解答:
设A(0,0),B(1,0),C(1,1),D(0,1),P(x,y),
则M=|PA|+|PD|+|PB|+|PC|
=(|PA|+|PC|)+(|PB|+|PD|)
=(|AP|+|PC|)+(|BP|+|PD|)
=(|
|+|
|)+(|
|+|
|)
≥|
+
|+|
+
|
=|
|+|
|
而
=(1,1)-(0,0)=(1,1),
=(0,1)-(1,0)=(-1,1)
∴|
|=
=
、|
|=
=
∴|
|+|
|=
+
=2
,
∴M≥
,
当
与
同向,
与
同向时取等号,设
=λ
,
=μ
,
代入坐标得1-x=λx,1-y=λy,-x=μx-μ,1-y=μy,解得λ=μ=1,x=y=
.
所以,当x=y=
时,M的最小值为2
.
则M=|PA|+|PD|+|PB|+|PC|
=(|PA|+|PC|)+(|PB|+|PD|)
=(|AP|+|PC|)+(|BP|+|PD|)
=(|
| AP |
| PC |
| BP |
| PD |
≥|
| AP |
| PC |
| BP |
| PD |
=|
| AC |
| BD |
而
| AC |
| BD |
∴|
| AC |
| 12+12 |
| 2 |
| BD |
| (-1)2+12 |
| 2 |
∴|
| AC |
| BD |
| 2 |
| 2 |
| 2 |
∴M≥
| 2 |
当
| AP |
| PC |
| BP |
| PD |
| PC |
| AP |
| PD |
| BP |
代入坐标得1-x=λx,1-y=λy,-x=μx-μ,1-y=μy,解得λ=μ=1,x=y=
| 1 |
| 2 |
所以,当x=y=
| 1 |
| 2 |
| 2 |
点评:本题主要考查平面向量的运用,长度可以看做向量的模是解题的关键.

练习册系列答案
相关题目
已知中心在原点,焦点在y轴上的双曲线的离心率为
,则它的渐近线方程为( )
| 5 |
| A、y=±2x | ||||
B、y=±
| ||||
C、y=±
| ||||
D、y=±
|
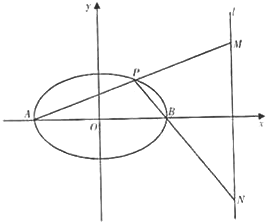 已知椭圆C:
已知椭圆C: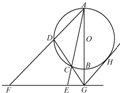 如图,AB是圆O的直径,G是AB延长线上的一点,GCD是圆O的割线,过点G作AG的垂线,交直线AC于点E,交直线 AD于点F,过点G作圆O的切线,切点为H.
如图,AB是圆O的直径,G是AB延长线上的一点,GCD是圆O的割线,过点G作AG的垂线,交直线AC于点E,交直线 AD于点F,过点G作圆O的切线,切点为H.