题目内容
设抛物线C：y2=2px（p＞0）的焦点F，准线为l，A为C上一点，以F为圆心且经过点A的圆交l于B、D两点，若∠ABD=90°，△ABF的面积为3
，则p=（ ）
| 3 |
| A、1 | ||
B、
| ||
| C、2 | ||
D、
|
考点：抛物线的简单性质
专题：计算题,直线与圆
分析：由题意，|AB|=|AF|=|BF|，△ABF是等边三角形，利用△ABF的面积为3
，求出|BF|，即可得出结论．
| 3 |
解答：
解：由题意，以F为圆心且经过点A的圆交l于B、D两点，∠ABD=90°，
∴|AB|=|AF|=|BF|，
∴△ABF是等边三角形，
∴∠FBD=30°．
∵△ABF的面积为3
，
∴|BF|=2
，
∴|DF|=
，即p=
．
故选：B．
∴|AB|=|AF|=|BF|，
∴△ABF是等边三角形，
∴∠FBD=30°．
∵△ABF的面积为3
| 3 |
∴|BF|=2
| 3 |
∴|DF|=
| 3 |
| 3 |
故选：B．
点评：本题考查抛物线的性质，考查抛物线的定义，考查学生的计算能力，比较基础．
练习册系列答案
综合自测系列答案
相关题目
设等比数列{an}的公比q=2，前n项和为Sn，则
=（ ）
| S5 |
| a4 |
| A、2 | ||
| B、4 | ||
C、
| ||
D、
|
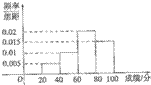某班的全体学生参加某项技能测试，成绩的频率分布直方图如图，数据的分组依次为：[20，40），[40，60），[60，80），[80，100]，若不低于80分的人数是8，则该班的学生人数是（ ）