题目内容
已知|
|=4,|
|=8,
与
的夹角为120°,则|2
-
|=( )
| a |
| b |
| a |
| b |
| a |
| b |
A、8
| ||
B、6
| ||
C、5
| ||
D、8
|
考点:数量积表示两个向量的夹角
专题:平面向量及应用
分析:把已知数据代入向量的模长公式计算可得.
解答:
解:∵|
|=4,|
|=8,
与
的夹角θ=120°,
∴|2
-
|=
=
=
=8
故选:A
| a |
| b |
| a |
| b |
∴|2
| a |
| b |
(2
|
4
|
=
4×42-4×4×8×(-
|
| 3 |
故选:A
点评:本题考查数量积与向量的夹角,涉及模长公式,属基础题.

练习册系列答案
相关题目
在△ABC中,角A,B,C的对边分别是a,b,c,且A,B,C成等差数列,a+c=2,则b的取值范围是( )
| A、[1,2) | ||
| B、(0,2] | ||
C、[1,
| ||
| D、[1,+∞) |
函数y=ax-1+2(a>0,且a≠1)的图象恒过点的坐标为( )
| A、(2,2) |
| B、(2,4) |
| C、(1,2) |
| D、(1,3) |
正数a,b满足ab=1,则a+2b的最小值为( )
A、
| ||
B、2
| ||
C、
| ||
| D、3 |
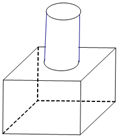 某机器零件是如图所示的几何体(实心),零件下面是边长为10cm的正方体,上面是底面直径为4cm,高为10cm的圆柱.
某机器零件是如图所示的几何体(实心),零件下面是边长为10cm的正方体,上面是底面直径为4cm,高为10cm的圆柱.