题目内容
设全集U={不超过5的正整数},A={x|x2-5x+q=0},B={x|x2+px+12=0},(∁UA)∪B={1,3,4,5},求p、q和集合A、B.
考点:交、并、补集的混合运算
专题:集合
分析:根据A补集与B的并集,得到元素2属于A,将x=2代入A中的方程求出q的值,确定出A,求出A的补集,得到元素3属于B,将x=3代入B求出p的值,确定出B即可.
解答:
解:全集U={1,2,3,4,5},A={x|x2-5x+q=0},B={x|x2+px+12=0},(∁UA)∪B={1,3,4,5},
∴2∈A,
将x=2代入x2-5x+q=0得:4-10+q=0,
即q=6,即x2-5x+6=0,
∴(x-2)(x-3)=0,即x=2或x=3,
∴A={2,3},∁UA={1,4,5},
∴3∈B,
将x=3代入x2+px+12=0得:9+3p+12=0,即p=-7,即x2-7x+12=0,
∴(x-3)(x-4)=0,即x=3或x=4,
∴B={3,4}.
∴2∈A,
将x=2代入x2-5x+q=0得:4-10+q=0,
即q=6,即x2-5x+6=0,
∴(x-2)(x-3)=0,即x=2或x=3,
∴A={2,3},∁UA={1,4,5},
∴3∈B,
将x=3代入x2+px+12=0得:9+3p+12=0,即p=-7,即x2-7x+12=0,
∴(x-3)(x-4)=0,即x=3或x=4,
∴B={3,4}.
点评:此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.

练习册系列答案
相关题目
已知一个正三棱锥的三条侧棱两两垂直且相等,底面边长为2,则该三棱锥的外接球的表面积是( )
| A、6π | B、12π |
| C、18π | D、24π |
已知集合A={x|-2≤x≤3},B={x|-1≤x≤4},那么集合A∩B等于( )
| A、{x|-2≤x≤4} |
| B、{x|3≤x≤4} |
| C、{x|-2≤x≤-1} |
| D、{x|-1≤x≤3} |
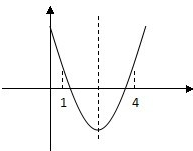 已知关于x不等式x2-2ax+a+2≤0(a∈R)的解集为M.
已知关于x不等式x2-2ax+a+2≤0(a∈R)的解集为M.