题目内容
k为何值时,直线y=kx+2和椭圆2x2+3y2=6有两个公共点?有一个公共点?没有公共点?
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:直线y=kx+2代入椭圆2x2+3y2=6,消去y,可得(2+3k2)x2+12kx+6=0,利用△>0、△=0、△<0,可得结论.
解答:
解:直线y=kx+2代入椭圆2x2+3y2=6,消去y,可得(2+3k2)x2+12kx+6=0,
∴△=144k2-24(2+3k2)=72k2-48,
①直线y=kx+2和椭圆2x2+3y2=6有两个交点,∴72k2-48>0,∴k>
或k<-
;
②直线y=kx+2和椭圆2x2+3y2=6有一个交点,∴72k2-48=0,∴k=±
;
③直线y=kx+2和椭圆2x2+3y2=6没有公共点,∴72k2-48<0,∴-
<k<
.
∴△=144k2-24(2+3k2)=72k2-48,
①直线y=kx+2和椭圆2x2+3y2=6有两个交点,∴72k2-48>0,∴k>
| ||
| 3 |
| ||
| 3 |
②直线y=kx+2和椭圆2x2+3y2=6有一个交点,∴72k2-48=0,∴k=±
| ||
| 3 |
③直线y=kx+2和椭圆2x2+3y2=6没有公共点,∴72k2-48<0,∴-
| ||
| 3 |
| ||
| 3 |
点评:本题考查直线和椭圆的位置关系,直线和椭圆的交点个数的判断方法,求出△=72k2-48,是解题的关键.

练习册系列答案
相关题目
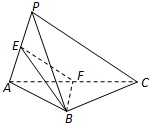 如图,在三棱锥P-ABC中,PA⊥PC,AB=PB,E,F分别是PA,AC的中点.求证:(1)EF∥平面PBC;
如图,在三棱锥P-ABC中,PA⊥PC,AB=PB,E,F分别是PA,AC的中点.求证:(1)EF∥平面PBC; 如图,以摩天轮中心为原点,水平方向为x轴建立平面直角坐标系,动点初始位于点P0(4,-3)处,现将其绕原点O逆时针旋转120°角到达点P处,则此时点P的纵坐标为
如图,以摩天轮中心为原点,水平方向为x轴建立平面直角坐标系,动点初始位于点P0(4,-3)处,现将其绕原点O逆时针旋转120°角到达点P处,则此时点P的纵坐标为