题目内容

在△ABC中，AB=2，AC=3，∠A=60°，P是三角形的内心，求
AP
•
BC
．
考点：平面向量数量积的运算
专题：平面向量及应用
分析：设AP延长线交BC于D，连接BP，内心的性质求得
BD
和
BC
关系，求得
AD
和
AB
，
AC
的关系式，求得|BD|，进而求得
|AP|
|AD|
，表示出
AP
，最后利用向量的数量积求得
AP
•
BC
解答： 解：设AP延长线交BC于D，连接BP，则
|AB|
|AC|
|BD|
|CD|
=
2
3
，
∴
BD
=
2
5
BC
=
2
5
（
AC
-
AB
）
AD
=
AB
+
BD
=
AB
+
2
5
BC
=
AB
+
2
5
（
AC
-
AB
）=
3
5
AB
+
2
5
AC
，
∴|
BD
|2=
4
25
[
AC
-
AB
]2=
4
25
（
AC
2-2
AC
•
AB
+
AB
2）=
4
25
（9-2×3×2×cos60°+4）=
28
25
，
∴|BD|=
2
7
5
，
|AP|
|PD|
=
|AP|
|AD|-|AP|
=
|AB|
|BD|
=
5
7
，
∴
|AP|
|AD|
=
5
5+
7
，
∴
AP
=
5
5+
7
，
AD
=
5
5+
7
•（
3
5
AB
+
2
5
AC
）=
1
5+
7
•（3
AB
+2
AC
），
∴
AP
•
BC
=
1
5+
7
•（3
AB
+2
AC
）•（
AC
-
AB
）=
1
5+
7
•（3
AB
•
AC
-3
AB
2+2
AC
2-2
AB
•
AC
=
1
5+
7
•（6+2•3•cos60°）=
5-
7
2
．
点评：本题主要考查了平面向量的数量积的运算．考查了学生推理和分析能力．
练习册系列答案
相关题目
双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的右焦点在直线l：ρsin（θ+
π
4
=
2
）（原点为极点、x轴正半轴为极轴）上，右顶点到直线l的距离为
2
2
，则双曲线C的渐近线方程为
 
．
在平面直角坐标系xOy中，已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）．四点（-
3
，
3
2
）、（1，
3
2
）、（
2
，0）、（
3
，-
3
2
）中有三点在椭圆C上．
（1）求椭圆C的方程；
（2）动直线l过点A（2，0），与y轴交于点R，与椭圆C交于点Q（Q不与A重合）．过原点O作直线l的平行线m，直线m与椭圆C的一个交点记为P．问：是否存在常数λ使得|AQ|、λ|OP|、|AR|成等比数列？若存在，请你求出实数λ的值；若不存在，请说明缘由．
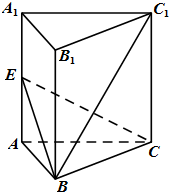如图，正三棱柱ABC-A1B1C1中，AA1=AB，E是侧棱AA1的中点．
（Ⅰ）证明：BC1⊥EC；
（Ⅱ）求二面角A-EC-B的余弦值．
已知函数f（x）=ax2-|x|+2a-1，（a≤
1
2
）． 
（1）若a=0，求函数f（x）的单调增区间；
（2）设f（x）在区间[1，2]上的最小值为g（a），求g（a）的表达式．
已知函数g（x）=alnx，f（x）=x3+x2+bx．
（1）若f（x）在区间[1，2]上不是单调函数，求实数b的范围；
（2）若对任意x∈[1，e]，都有g（x）≥-x2+（a+2）x恒成立，求实数a的取值范围；
（3）当b=0时，设F（x）=
f(-x)，x＜1
g(x)，x≥1
，对任意给定的正实数a，曲线y=F（x）上是否存在两点P，Q，使得△POQ是以O（O为坐标原点）为直角顶点的直角三角形，而且此三角形斜边中点在y轴上？请说明理由．
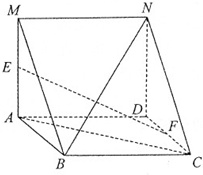如图，四边形ABCD是菱形，四边形MADN是矩形，平面MADN⊥平面ABCD，E，F分别为MA，DC的中点，求证：
（Ⅰ）EF∥平面MNCB；
（Ⅱ）平面MAC⊥平面BND．
k为何值时，直线y=kx+2和椭圆2x2+3y2=6有两个公共点？有一个公共点？没有公共点？
在一次口试中，要从10道题中随机抽出3道题进行回答，答对其中两道或两道以上的题可获得及格．某考生会回答10道题中的6道题，那么他（她）获得及格的概率是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网