题目内容
已知P(x,y)为圆x2+y2=4上任意一点,则x+y的最大值为 .
考点:直线与圆的位置关系
专题:直线与圆
分析:设t=x+y,则y=t-x,则可得到x2+(t-x)2=4,整理得2x2-4tx+t2-4=0,此方程有解,根据判别式的意义得到△≥0,即可求解x+y的最大值.
解答:
解:设t=x+y,则y=t-x,
∵x2+y2=4,
∴x2+(t-x)2=4,
整理得2x2-2tx+t2-4=0,
∵x为实数,
∴△=4t2-4×2(t2-4)≥0,即t2≤8,
∴-2
≤t≤2
,
∴x+y的最大值为:2
.
故答案为:2
.
∵x2+y2=4,
∴x2+(t-x)2=4,
整理得2x2-2tx+t2-4=0,
∵x为实数,
∴△=4t2-4×2(t2-4)≥0,即t2≤8,
∴-2
| 2 |
| 2 |
∴x+y的最大值为:2
| 2 |
故答案为:2
| 2 |
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
已知集合A={y|x2+y2=1},B={y|y=x},则A∩B=( )
A、{(-
| ||||||||||||||||
B、{-
| ||||||||||||||||
| C、[-1,1] | ||||||||||||||||
| D、{-1,1} |
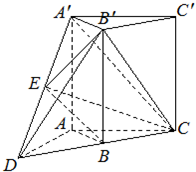 如图,直三棱柱A′B′C′-ABC,延长CB到点D,使BD=BC,点E为A′D的中点,∠ABC=90°,AB=BC=
如图,直三棱柱A′B′C′-ABC,延长CB到点D,使BD=BC,点E为A′D的中点,∠ABC=90°,AB=BC=