题目内容
 如图,以摩天轮中心为原点,水平方向为x轴建立平面直角坐标系,动点初始位于点P0(4,-3)处,现将其绕原点O逆时针旋转120°角到达点P处,则此时点P的纵坐标为
如图,以摩天轮中心为原点,水平方向为x轴建立平面直角坐标系,动点初始位于点P0(4,-3)处,现将其绕原点O逆时针旋转120°角到达点P处,则此时点P的纵坐标为考点:两角和与差的正弦函数
专题:三角函数的求值
分析:记∠xOP0=α,可得cosα=
,sinα=-
,进而可得sin(α+120°的值,再乘以圆的半径即可.
| 4 |
| 5 |
| 3 |
| 5 |
解答:
解:记∠xOP0=α,由三角函数的定义可得cosα=
,sinα=-
,
又由题意可得OP为α+120°的终边,
∴sin(α+120°)=-
sinα+
cosα
=-
×(-
)+
×
=
∴此时点P的纵坐标为:5×
=
故答案为:
| 4 |
| 5 |
| 3 |
| 5 |
又由题意可得OP为α+120°的终边,
∴sin(α+120°)=-
| 1 |
| 2 |
| ||
| 2 |
=-
| 1 |
| 2 |
| 3 |
| 5 |
| ||
| 2 |
| 4 |
| 5 |
3+4
| ||
| 10 |
∴此时点P的纵坐标为:5×
3+4
| ||
| 10 |
3+4
| ||
| 2 |
故答案为:
3+4
| ||
| 2 |
点评:本题考查两角和与差的正弦函数,属基础题.

练习册系列答案
相关题目
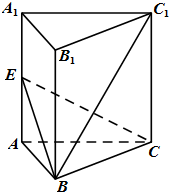 如图,正三棱柱ABC-A1B1C1中,AA1=AB,E是侧棱AA1的中点.
如图,正三棱柱ABC-A1B1C1中,AA1=AB,E是侧棱AA1的中点.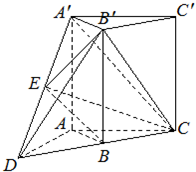 如图,直三棱柱A′B′C′-ABC,延长CB到点D,使BD=BC,点E为A′D的中点,∠ABC=90°,AB=BC=
如图,直三棱柱A′B′C′-ABC,延长CB到点D,使BD=BC,点E为A′D的中点,∠ABC=90°,AB=BC=