题目内容
已知直线x=my+1过椭圆C:
+
=1(a>b>0)的右焦点F2,且交椭圆于A,B两点,已知椭圆的离心率为方程2x2+x-1=0的实根,F1为椭圆的左焦点,
(1)求证:△F1AB的周长为定值,并求出定值;
(2)当△F1AB的内切圆半径最大时,求m的值.
| x2 |
| a |
| y2 |
| b |
(1)求证:△F1AB的周长为定值,并求出定值;
(2)当△F1AB的内切圆半径最大时,求m的值.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)解方程2x2+x-1=0,得椭圆C:
+
=1(a>b>0)的离心率为e=
=
,由直线x=my+1过椭圆C:
+
=1(a>b>0)的右焦点F2,得k=1,由此能求出△F1AB的周长为定值,定值为8.
(2)△F1AB的内切圆半径最大时,|AF2|=|BF2|,由此能求出m=0.
| x2 |
| a |
| y2 |
| b |
| c |
| a |
| 1 |
| 2 |
| x2 |
| a |
| y2 |
| b |
(2)△F1AB的内切圆半径最大时,|AF2|=|BF2|,由此能求出m=0.
解答:
(1)证明:解方程2x2+x-1=0,得x1=-1,x 2=
,
由题意知椭圆C:
+
=1(a>b>0)的离心率为e=
=
,
∴a=2k,b=
k,c=k,(k>0),∴F2(k,0),
∵直线x=my+1过椭圆C:
+
=1(a>b>0)的右焦点F2,
∴k=1,∴椭圆方程为
+
=1,
∴△F1AB的周长L=4a=8,
∴△F1AB的周长为定值,定值为8.
(2)解:△F1AB的内切圆半径最大时,
|AF2|=|BF2|,
此时直线方程为x=my+1=1,
解得m=0.
| 1 |
| 2 |
由题意知椭圆C:
| x2 |
| a |
| y2 |
| b |
| c |
| a |
| 1 |
| 2 |
∴a=2k,b=
| 3 |
∵直线x=my+1过椭圆C:
| x2 |
| a |
| y2 |
| b |
∴k=1,∴椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
∴△F1AB的周长L=4a=8,
∴△F1AB的周长为定值,定值为8.
(2)解:△F1AB的内切圆半径最大时,
|AF2|=|BF2|,
此时直线方程为x=my+1=1,
解得m=0.
点评:本题考查三角形周长为定值的证明,考查三角形内切圆半径最大时实数值的求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
相关题目
设实数a,b,c满足a+b+c=0,则a,b,c中( )
| A、至多有一个不大于0 |
| B、至少有一个不小于0 |
| C、至多有两个不小于0 |
| D、至少有两个不小于0 |
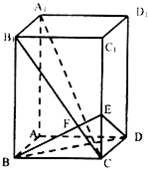 已知长方体AC1中,棱AB=BC=1,棱BB1=2,连结B1C,过B点作B1C的垂线交CC1于E,交B1C于F.
已知长方体AC1中,棱AB=BC=1,棱BB1=2,连结B1C,过B点作B1C的垂线交CC1于E,交B1C于F. 小华参加学校创意社团,上交一份如图所示的作品:边长为2的正方形中作一内切圆⊙O,在⊙O内作一个关于正方形对角线对称的内接“十”字形图案.OA垂直于该“十”字形图案的一条边,点P为该边上的一个端点.记“十”字形图案面积为S,∠AOP=θ.试用θ表示S,并由此求出S的最大值.
小华参加学校创意社团,上交一份如图所示的作品:边长为2的正方形中作一内切圆⊙O,在⊙O内作一个关于正方形对角线对称的内接“十”字形图案.OA垂直于该“十”字形图案的一条边,点P为该边上的一个端点.记“十”字形图案面积为S,∠AOP=θ.试用θ表示S,并由此求出S的最大值.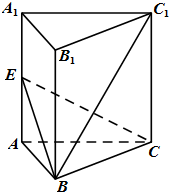 如图,正三棱柱ABC-A1B1C1中,AA1=AB,E是侧棱AA1的中点.
如图,正三棱柱ABC-A1B1C1中,AA1=AB,E是侧棱AA1的中点.