题目内容
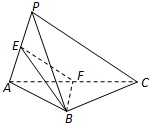如图，在三棱锥P-ABC中，PA⊥PC，AB=PB，E，F分别是PA，AC的中点．求证：（1）EF∥平面PBC；（2）平面BEF⊥平面PAB．
考点：平面与平面垂直的判定,直线与平面平行的判定
专题：空间位置关系与距离
分析：（1）由三角形中位线定理推导出EF∥PC，由此能证明EF∥平面PBC．
（2）由已知条件推导出PA⊥BE，PA⊥EF，由此能证明平面PAB⊥平面BEF．
（2）由已知条件推导出PA⊥BE，PA⊥EF，由此能证明平面PAB⊥平面BEF．
解答：
证明：（1）在△APC中，
因为E，F分别是PA，AC的中点，
所以EF∥PC，…（3分）
又PC?平面PAC，EF?平面PAC，
所以EF∥平面PBC； …（6分）
（2）因为AB=PB，且点E是PA的中点，所以PA⊥BE； …（9分）
又PA⊥PC，EF∥PC，所以PA⊥EF，…（12分）
因为BE?平面BEF，EF?平面BEF，
BE∩EF=E，PA?平面PAB，
所以平面PAB⊥平面BEF．…（14分）
因为E，F分别是PA，AC的中点，
所以EF∥PC，…（3分）
又PC?平面PAC，EF?平面PAC，
所以EF∥平面PBC； …（6分）
（2）因为AB=PB，且点E是PA的中点，所以PA⊥BE； …（9分）
又PA⊥PC，EF∥PC，所以PA⊥EF，…（12分）
因为BE?平面BEF，EF?平面BEF，
BE∩EF=E，PA?平面PAB，
所以平面PAB⊥平面BEF．…（14分）
点评：本题考查直线与平面平行的证明，考查平面与平面垂直的证明，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
小华参加学校创意社团，上交一份如图所示的作品：边长为2的正方形中作一内切圆⊙O，在⊙O内作一个关于正方形对角线对称的内接“十”字形图案．OA垂直于该“十”字形图案的一条边，点P为该边上的一个端点．记“十”字形图案面积为S，∠AOP=θ．试用θ表示S，并由此求出S的最大值．