题目内容
4.已知x>0,y>0,8x+2y-xy=0,则x+y的最小值为18.分析 已知式子变形可得$\frac{8}{y}$+$\frac{2}{x}$=1,整体代入可得x+y=(x+y)($\frac{8}{y}$+$\frac{2}{x}$)=10+$\frac{2y}{x}$+$\frac{8x}{y}$,由基本不等式可得.
解答 解:∵x>0,y>0,8x+2y-xy=0,
∴$\frac{8}{y}$+$\frac{2}{x}$-1=0,即$\frac{8}{y}$+$\frac{2}{x}$=1,
∴x+y=(x+y)($\frac{8}{y}$+$\frac{2}{x}$)
=10+$\frac{2y}{x}$+$\frac{8x}{y}$≥10+2$\sqrt{\frac{2y}{x}•\frac{8x}{y}}$=18,
当且仅当$\frac{2y}{x}$=$\frac{8x}{y}$即x=6且y=12时取等号.
故答案为:18.
点评 本题考查基本不等式求最值,变形并整体代入是解决问题的关键,属基础题.

练习册系列答案
相关题目
14.点P(2,0)关于直线x+y+1=0对称点Q的坐标为( )
| A. | (-1,-3) | B. | (3,3) | C. | (-1,3) | D. | (4,-2) |
15.已知点C(3,4),抛物线y2=8x的准线为L,设抛物线上任意一点P到直线L的距离为m,则m+|PC|的最小值为( )
| A. | 5 | B. | $\sqrt{41}$ | C. | $\sqrt{41}$-2 | D. | 4 |
13.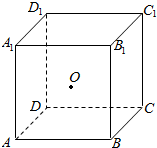 正方体ABCD-A1B1C1D1边长为2,O为正方体的中心,动点P在正方体底面ABCD内运动(包括边界),若AO⊥OP,则点P的轨迹为( )
正方体ABCD-A1B1C1D1边长为2,O为正方体的中心,动点P在正方体底面ABCD内运动(包括边界),若AO⊥OP,则点P的轨迹为( )
 正方体ABCD-A1B1C1D1边长为2,O为正方体的中心,动点P在正方体底面ABCD内运动(包括边界),若AO⊥OP,则点P的轨迹为( )
正方体ABCD-A1B1C1D1边长为2,O为正方体的中心,动点P在正方体底面ABCD内运动(包括边界),若AO⊥OP,则点P的轨迹为( )| A. | 椭圆的一部分 | B. | 线段 | C. | 圆的部分 | D. | 抛物线的一部分 |
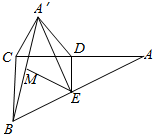 已知在△ABC中,D,E分别为AC,AB的中点,沿DE将△ADE折起,使A到A′的位置,若M是A′B的中点,求证:ME∥平面A′CD.
已知在△ABC中,D,E分别为AC,AB的中点,沿DE将△ADE折起,使A到A′的位置,若M是A′B的中点,求证:ME∥平面A′CD. 如图,ABCD是边长为2的正方形,ED=1,DE⊥平面ABCD,EF∥BD,且EF=$\frac{1}{2}$BD.
如图,ABCD是边长为2的正方形,ED=1,DE⊥平面ABCD,EF∥BD,且EF=$\frac{1}{2}$BD.