Question

13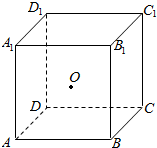．正方体ABCD-A₁B₁C₁D₁边长为2，O为正方体的中心，动点P在正方体底面ABCD内运动（包括边界），若AO⊥OP，则点P的轨迹为（　　）

• A． 椭圆的一部分
• B． 线段
• C． 圆的部分
• D． 抛物线的一部分

Answer 1

分析 根据题意，建立空间直角坐标系，利用向量的数量积为0，得出点P的轨迹方程，即可得出点P的轨迹是什么图形．

解答 解：以DA所在的直线为x轴，DC所在的直线为y轴，DD₁所在的直线为z轴，
建立空间直角坐标系，如图所示；
又正方体ABCD-A₁B₁C₁D₁棱长为2，
∴正方体的中心O（1，1，1），
A（2，0，0）；
设平面ABCD内的动点为P（x，y，0），
则$\overrightarrow{AO}$=（-1，1，1），$\overrightarrow{OP}$=（x-1，y-1，-1）；
∵AO⊥OP，即$\overrightarrow{AO}$⊥$\overrightarrow{OP}$，
∴$\overrightarrow{AO}$•$\overrightarrow{OP}$=-（x-1）+（y-1）-1=0，
化简得x-y+1=0；
又点P在平面xoy内，且x∈[0，1]，y∈[0，1]，
∴x-y+1=0表示线段，即点P的轨迹为线段．
故选：B．

点评 本题考查了空间几何体的应用问题，也考查了空间想象能力与转化思想的应用问题，是综合性题目．