题目内容
命题“任意x∈R，x2+2x+2＞0”的否定是（ ）
| A、任意x∈R，x2+2x+2≤0 |
| B、不存在x∈R，x2+2x+2＞0 |
| C、存在x∈R，x2+2x+2≤0 |
| D、存在x∈R，x2+2x+2＞0 |
考点：命题的否定
专题：简易逻辑
分析：利用全称命题的否定是特称命题，写出结果即可．
解答：
解：因为全称命题的否定是特称命题，
所以命题“任意x∈R，x2+2x+2＞0”的否定是：存在x∈R，x2+2x+2≤0．
故选：C．
所以命题“任意x∈R，x2+2x+2＞0”的否定是：存在x∈R，x2+2x+2≤0．
故选：C．
点评：本题考查命题的否定，全称命题与特称命题的否定关系，基本知识的考查．
练习册系列答案
阅读快车系列答案
相关题目
已知：△ABC中，若a2=b2-c2-
ac，则角B=（ ）
| 3 |
| A、150° | B、120° |
| C、60° | D、30° |
如图所示的程序框图的输入值x∈[-1，3]，则输出值y的取值范围为（ ）
| A、[1，2] |
| B、[0，2] |
| C、[0，1] |
| D、[-1，2] |
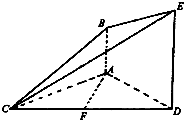如图，已知DE⊥平面ACD，DE∥AB，△ACD是正三角形，AD=DE=2AB=2，且F是CD的中点．