题目内容
19．设A={x|y=$\sqrt{2-x}$}，B={y|y=1n（1+x）}，则A∩B=（-∞，2]．分析 先化简A，B，再求出A∩B．
解答 解：∵A={x|y=$\sqrt{2-x}$}=（-∞，2]，B={y|y=1n（1+x）}=R，
∴A∩B=（-∞，2]，
故答案为：（-∞，2]
点评 本题考查函数的定义域、值域，考查集合的运算，比较基础．
练习册系列答案
相关题目
9．若$\overrightarrow{OA}$=（3，2），$\overrightarrow{OB}$=（-4，y），并且$\overrightarrow{OB}$⊥$\overrightarrow{OA}$，则|$\overrightarrow{OB}$|=（ ）
| A． | $\sqrt{13}$ | B． | 4$\sqrt{13}$ | C． | 2$\sqrt{13}$ | D． | 2$\sqrt{11}$ |
4．
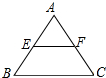在三角形ABC中，E、F分别是AB、AC的中点，若在三角形内部，随机取一点Q，则点Q取自△AEF内部的概率是（ ）
在三角形ABC中，E、F分别是AB、AC的中点，若在三角形内部，随机取一点Q，则点Q取自△AEF内部的概率是（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |