题目内容
过点(1,-2)且倾斜角的余弦是-
的直线方程是 .
| 3 |
| 5 |
考点:直线的点斜式方程
专题:直线与圆
分析:利用同角三角函数基本关系式可得斜率,再利用点斜式即可得出.
解答:
解:设直线的倾斜角为θ,θ∈[0,π).
∵cosθ=-
,
∴sinθ=
,tanθ=
=-
.
∴要求的直线方程为:y+2=-
(x-1),化为4x+3y+2=0.
故答案为:4x+3y+2=0.
∵cosθ=-
| 3 |
| 5 |
∴sinθ=
| 4 |
| 5 |
| sinθ |
| cosθ |
| 4 |
| 3 |
∴要求的直线方程为:y+2=-
| 4 |
| 3 |
故答案为:4x+3y+2=0.
点评:本题考查了同角三角函数基本关系式、斜率、点斜式,考查了计算能力,属于基础题.

练习册系列答案
相关题目
函数y=
的图象大致是( )
| x3 |
| 3x-1 |
A、 |
B、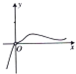 |
C、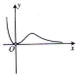 |
D、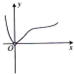 |
曲线y=e
x在点(4,e2)处的切线与坐标轴所围三角形的面积为( )
| 1 |
| 2 |
| A、e2 | ||
| B、2e2 | ||
| C、4e2 | ||
D、
|