题目内容
若f（x）=
，x1＜x2＜x3，且f （x1）=f （x2）=f （x3），则x1+x2+x3的值的范围是（ ）
|
| A、[1，2） |
| B、（1，2] |
| C、（0，1] |
| D、[2，3） |
考点：分段函数的应用
专题：计算题,数形结合,函数的性质及应用
分析：画出分段函数的图象，由二次函数的对称性可得x2+x3=2，即有x1+x2+x3=x1+2，再由图象解得-1≤x1＜0，进而得到所求范围．
解答：
解：由于f（x）=
，
当x＜0时，y＞-2；
当x≥0时，y=（x-1）2-2≥-2，
f（0）=f（2）=-1，
由x1＜x2＜x3，且f （x1）=f （x2）=f （x3），
则x2+x3=2，即有x1+x2+x3=x1+2，
当f（x1）=-1即-x1-2=-1，解得x1=-1，
由-1≤x1＜0，
可得1≤x1+2＜2，
故选：A．
解：由于f（x）=
|
当x＜0时，y＞-2；
当x≥0时，y=（x-1）2-2≥-2，
f（0）=f（2）=-1，
由x1＜x2＜x3，且f （x1）=f （x2）=f （x3），
则x2+x3=2，即有x1+x2+x3=x1+2，
当f（x1）=-1即-x1-2=-1，解得x1=-1，
由-1≤x1＜0，
可得1≤x1+2＜2，
故选：A．
点评：本题考查分段函数的图象和应用，考查二次函数的对称性，考查数形结合的思想方法，属于中档题和易错题．
练习册系列答案
相关题目
若x2+y2=4则x-y的最大值是（ ）
| A、2 | ||
B、2
| ||
| C、4 | ||
D、4
|
函数y=
的图象大致是（ ）
| x3 |
| 3x-1 |
A、 |
B、 |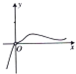
C、 |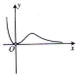
D、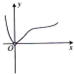 |