题目内容
 如图,设α∈(0,π),且α≠
如图,设α∈(0,π),且α≠| π |
| 2 |
| e1 |
| e2 |
| OP |
| e1 |
| e2 |
| OP |
①设
| a |
| b |
| a |
| b |
②设
| a |
| a |
| m2+n2 |
③设
| a |
| b |
| a |
| b |
④设
| a |
| b |
| a |
| b |
⑤设
| a |
| b |
| a |
| b |
| π |
| 3 |
| 2π |
| 3 |
考点:进行简单的合情推理
专题:综合题,平面向量及应用
分析:把新定义回归到向量的数量积的运算对每个结论进行验证,即可得出结论.
解答:
解:显然①正确;
|
|=|m
+n
|=
,∵α≠≠
,∴②错误;
由
∥
得
=λ
,∴s=λm,t=λn,∴mt-ns=0,故③正确;
∵
•
=(m
+n
)•(s
+t
)=ms+nt+(mt+ns)cosα≠ms+nt,∴④错误;
根据夹角公式得4+5
•
=(5+4
•
)cos
,故
•
=-
,即cosα=-
,则α=
⑤正确
所以正确的是①、③、⑤.
|
| a |
| e1 |
| e2 |
| m2+n2+2mncosα |
| π |
| 2 |
由
| a |
| b |
| b |
| a |
∵
| a |
| b |
| e1 |
| e2 |
| e1 |
| e2 |
根据夹角公式得4+5
| e1 |
| e2 |
| e1 |
| e2 |
| π |
| 3 |
| e1 |
| e2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2π |
| 3 |
所以正确的是①、③、⑤.
点评:本题为新定义,正确理解题中给出的斜坐标并与已知的向量知识相联系是解决问题的关键,属基础题.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
函数f(x)在点x=x0处连续是f(x)在x=x0处可导的( )
| A、必要条件 |
| B、充分条件 |
| C、充分必要条件 |
| D、既非充分条件又非必要条件 |
若复数z满足z(1+i)=i(i为虚数单位),则z为( )
A、
| ||
B、
| ||
| C、1+i | ||
| D、1-i |
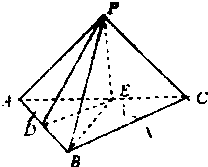 如图,在三棱锥P-ABC中,AB=2,AC=BC=
如图,在三棱锥P-ABC中,AB=2,AC=BC=