题目内容
函数f(x)在点x=x0处连续是f(x)在x=x0处可导的( )
| A、必要条件 |
| B、充分条件 |
| C、充分必要条件 |
| D、既非充分条件又非必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据函数连续和函数可导的定义,结合充分条件和必要条件的定义即可得到结论.
解答:
解:由“函数y=f(x)在x=x0处连续”,不能推出“函数y=f(x)在x=x0处可导”,
例如函数y=|x|在x=0处连续,但不可导.
而由“函数y=f(x)在x=x0处可导”,可得“函数y=f(x)在x=x0处连续”.
故“函数y=f(x)在x=x0处连续”是“函数y=f(x)在x=x0处可导”的必要不充分条件,
故选A.
例如函数y=|x|在x=0处连续,但不可导.
而由“函数y=f(x)在x=x0处可导”,可得“函数y=f(x)在x=x0处连续”.
故“函数y=f(x)在x=x0处连续”是“函数y=f(x)在x=x0处可导”的必要不充分条件,
故选A.
点评:本题主要考查充分条件和必要条件的判断,利用函数可导和函数连续的定义和性质是解决本题的关键.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
商场人流量被定义为每分钟通入口的人数,五一某商场的人流量满足函数F(t)=50+4sin
(t≥0),则在下列哪个时间段内人流量是增加的( )
| t |
| 2 |
| A、[0,5] |
| B、[5,10] |
| C、[10,15] |
| D、[15,20] |
已知a、b∈R,且ab≠0,则下列结论恒成立的是( )
A、a+b≥2
| ||||
B、
| ||||
C、|
| ||||
| D、a2+b2>2ab |
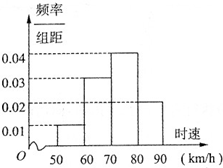 某地区对某路段公路上行驶的汽车速度实施监控,从中抽取50辆汽车进行测速分析,得到如图所示的时速的频率分布直方图,根据该图,时速在70km/h以下的汽车有
某地区对某路段公路上行驶的汽车速度实施监控,从中抽取50辆汽车进行测速分析,得到如图所示的时速的频率分布直方图,根据该图,时速在70km/h以下的汽车有 如图,设α∈(0,π),且α≠
如图,设α∈(0,π),且α≠