题目内容
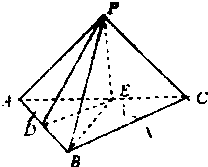 如图,在三棱锥P-ABC中,AB=2,AC=BC=
如图,在三棱锥P-ABC中,AB=2,AC=BC=| 10 |
(1)求证:BC∥平面PDE;
(2)求直线BE与平面PAB所成角的大小.
考点:与二面角有关的立体几何综合题,直线与平面平行的判定,直线与平面所成的角
专题:空间角
分析:(1)由D、E分别是AB、AC的中点,得到在△ABC中,DE是中位线,由此能够证明BC∥平面PDE.
(2)连结CD,交BE于O,过O作OF⊥PD,交PD于F,由已知条件推导出∠PDC是二面角P-AB-C的平面角,由此能求出直线BE与平面PAB所成角的大小.
(2)连结CD,交BE于O,过O作OF⊥PD,交PD于F,由已知条件推导出∠PDC是二面角P-AB-C的平面角,由此能求出直线BE与平面PAB所成角的大小.
解答:
(1)证明:∵D、E分别是AB、AC的中点,
∴在△ABC中,DE是中位线,
∴DE∥BC,
∵DE?平面PDE,BC不包含于平面PDE,
∴BC∥平面PDE.
(2)解:如图,连结CD,交BE于O,过O作OF⊥PD,交PD于F,
∵AB=2,AC=BC=
,PA=PB,二面角P-AB-C的大小为45°,
D、E分别是AB、AC的中点,
∴PD⊥AB,CD⊥AB,
∴∠PDC是二面角P-AB-C的平面角,∴∠FDO=45°,
∵PD∩CD=D,∴AB⊥平面PCD,
∵OF?平面PCD,∴OF⊥AB,
又∵OF⊥PD,PD∩AB=D,∴OF⊥平面PAB,
∴∠OBF是直线BF与平面PAB所成角的平面角.
∵CD=
=3,∴OD=
CD=1,
∴DF=OF=1•sin45°=
,BF=
=
=
,
∴sin∠OBF=
=
=
,
∴∠OBF=arcsin
.
∴直线BE与平面PAB所成角的大小是arcsin
.
∴在△ABC中,DE是中位线,
∴DE∥BC,

∵DE?平面PDE,BC不包含于平面PDE,
∴BC∥平面PDE.
(2)解:如图,连结CD,交BE于O,过O作OF⊥PD,交PD于F,
∵AB=2,AC=BC=
| 10 |
D、E分别是AB、AC的中点,
∴PD⊥AB,CD⊥AB,
∴∠PDC是二面角P-AB-C的平面角,∴∠FDO=45°,
∵PD∩CD=D,∴AB⊥平面PCD,
∵OF?平面PCD,∴OF⊥AB,
又∵OF⊥PD,PD∩AB=D,∴OF⊥平面PAB,
∴∠OBF是直线BF与平面PAB所成角的平面角.
∵CD=
(
|
| 1 |
| 3 |
∴DF=OF=1•sin45°=
| ||
| 2 |
| DF2+BD2 |
|
| ||
| 2 |
∴sin∠OBF=
| OF |
| BF |
| ||||
|
| ||
| 3 |
∴∠OBF=arcsin
| ||
| 3 |
∴直线BE与平面PAB所成角的大小是arcsin
| ||
| 3 |
点评:本题考查直线与平面平行的证明,考查直线与平面所成角的大小的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
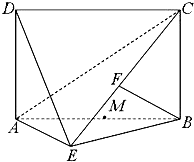 四边形ABCD为矩形,∠AEB=
四边形ABCD为矩形,∠AEB= 如图,设α∈(0,π),且α≠
如图,设α∈(0,π),且α≠