题目内容
用单调性定义证明函数f(x)=
在(-1,+∞)上是增函数.
| x-2 |
| x+1 |
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:根据函数单调性的定义按五步走证明即可.
解答:
解:∵f(x)=
=1-
,
设x1,x2∈(-1,+∞),且x1<x2,
∴f(x1)-f(x2)=1-
-1+
=
,
因为-1<x1<x2,
所以x1-x2<0,x1+1>0,x2+1>0,
所以f(x1)-f(x2)<0,
即f(x1)<f(x2),
故函数f(x)=
在(-1,+∞)上是增函数.
| x-2 |
| x+1 |
| 3 |
| x+1 |
设x1,x2∈(-1,+∞),且x1<x2,
∴f(x1)-f(x2)=1-
| 3 |
| x1+1 |
| 3 |
| x2+1 |
| 3(x1-x2) |
| (x1+1)(x2+1) |
因为-1<x1<x2,
所以x1-x2<0,x1+1>0,x2+1>0,
所以f(x1)-f(x2)<0,
即f(x1)<f(x2),
故函数f(x)=
| x-2 |
| x+1 |
点评:本题考查的知识点是函数的单调性的判断与证明,利用定义法(作差法)证明单调性的步骤是:设元→作差→分解→断号→结论.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
要得到函数y=2cos(2x-
)的图象,只需将函数y=2sin2x的图象( )
| π |
| 3 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
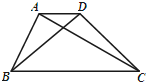 如图,在梯形ABCD中,AD∥BC,AB=5,AC=9,∠BCA=30°,∠ADB=45°.
如图,在梯形ABCD中,AD∥BC,AB=5,AC=9,∠BCA=30°,∠ADB=45°.