题目内容
已知函数f(x)=
sin(x+
),求函数:
(1)最小正周期;
(2)对称中心;
(3)单调递增区间.
| 3 |
| π |
| 6 |
(1)最小正周期;
(2)对称中心;
(3)单调递增区间.
考点:正弦函数的单调性,三角函数的周期性及其求法,正弦函数的对称性
专题:三角函数的图像与性质
分析:对于函数f(x)=
sin(x+
),根据正弦函数的周期性、图象的对称性、单调性,得出结论.
| 3 |
| π |
| 6 |
解答:
解:对于函数f(x)=
sin(x+
),(1)显然函数的周期为T=2π.
(2)令x+
=kπ,k∈z,求得x=kπ-
,k∈z,可得函数的图象的对称中心为 (kπ-
,0),(k∈Z).
(3)令2kπ-
≤x+
≤2kπ+
,k∈z,求得 2kπ-
≤x+
≤2kπ+
,k∈z,
故函数的递增区间为 [2kπ-
,2kπ+
],(k∈Z).
| 3 |
| π |
| 6 |
(2)令x+
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
(3)令2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| 2π |
| 3 |
| π |
| 6 |
| π |
| 3 |
故函数的递增区间为 [2kπ-
| 2π |
| 3 |
| π |
| 3 |
点评:本题主要考查正弦函数的周期性、图象的对称性、单调性,属于基础题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
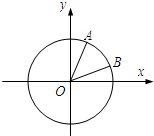 如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边
如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边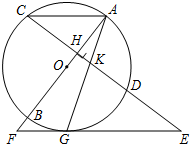 如图,AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K,连接AC,且KG2=KD•GE.
如图,AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K,连接AC,且KG2=KD•GE.