题目内容
已知圆C过A（1，4）、B（3，2）两点，且圆心在直线y=0上．
（1）求圆C的方程；
（2）判断点P（2，4）与圆C的位置关系．
（1）求圆C的方程；
（2）判断点P（2，4）与圆C的位置关系．
考点：圆的标准方程,点与圆的位置关系
专题：直线与圆
分析：（1）求出圆心和半径，即可求圆C的方程；
（2）根据点P（2，4）与圆C的位置关系，即可得到结论．
（2）根据点P（2，4）与圆C的位置关系，即可得到结论．
解答：
解：（1）∵圆心在直线y=0上，
∴设圆心坐标为C（a，0），
则|AC|=|BC|，
即
=
，
即（a-1）2+16=（a-3）2+4，
解得a=-1，即圆心为（-1，0），
半径r=|AC|=
=
=2
，
则圆的标准方程为（x+1）2+y2=20，
（2）∵|PC|=
=
=
=5＞r，
∴点P（2，4）在圆C的外面．
∴设圆心坐标为C（a，0），
则|AC|=|BC|，
即
| (a-1)2+16 |
| (a-3)2+4 |
即（a-1）2+16=（a-3）2+4，
解得a=-1，即圆心为（-1，0），
半径r=|AC|=
| (-1-1)2+16 |
| 20 |
| 5 |
则圆的标准方程为（x+1）2+y2=20，
（2）∵|PC|=
| (-1-2)2+(0-4)2 |
| 9+16 |
| 25 |
∴点P（2，4）在圆C的外面．
点评：本题主要考查圆的方程的求解，根据条件求出圆心和半径是解决本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
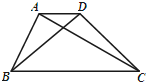如图，在梯形ABCD中，AD∥BC，AB=5，AC=9，∠BCA=30°，∠ADB=45°．
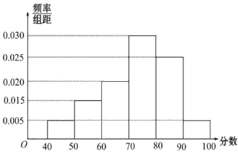某校从参加高二年级学业水平测试的学生中抽出80名学生，其数学成绩（均为整数）的频率分布直方图如图所示．