题目内容
已知函数f(x)=ax+lnx,x∈(1,e).
(1)若f(x)≤0恒成立,求a的取值范围;
(2)若方程f(x)=-
有两个不等实根,求a的取值范围.
(1)若f(x)≤0恒成立,求a的取值范围;
(2)若方程f(x)=-
| 1 |
| 2 |
考点:利用导数求闭区间上函数的最值
专题:计算题,导数的综合应用
分析:(1)将恒成立问题化为最值问题,求导后求最值;(2)方程的根转化为函数图象的交点.
解答:
解:(1)∵ax+lnx≤0,x∈(1,e);
∴a≤-
,
令g(x)=-
,则g′(x)=
=
,
∵x∈(1,e),∴g′(x)<0;
∴g(x)在(1,e)上是减函数,
∴a<-
.
(2)由题意,ax+lnx=-
;
则方程f(x)=-
有两个不等实根可化为函数y=-ax-
的图象与函数y=lnx的图象有两个交点,
由k1=
=
,k2=
=
>
,
又由
=
,则k3=
;
则
<-a<
,
则-
<a<-
.
∴a≤-
| lnx |
| x |
令g(x)=-
| lnx |
| x |
-
| ||
| x2 |
| lnx-1 |
| x2 |
∵x∈(1,e),∴g′(x)<0;
∴g(x)在(1,e)上是减函数,
∴a<-
| 1 |
| e |
(2)由题意,ax+lnx=-
| 1 |
| 2 |
则方程f(x)=-
| 1 |
| 2 |
| 1 |
| 2 |
由k1=
0+
| ||
| 1-0 |
| 1 |
| 2 |
1+
| ||
| e-0 |
| 3 |
| 2e |
| 1 |
| 2 |
又由
lnx+
| ||
| x |
| 1 |
| x |
| 1 | ||
|
则
| 3 |
| 2e |
| 1 | ||
|
则-
| 1 | ||
|
| 3 |
| 2e |
点评:本题考查了函数的导数综合应用,恒成立要转化为最值问题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
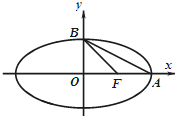 如图,椭圆C:
如图,椭圆C: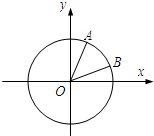 如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边
如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边