��Ŀ����
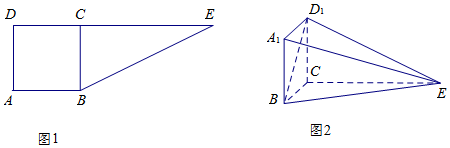
2���ڡ�ABC�У������Ҷ�����$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$=��ֵ�������ֵ���ǡ�ABC�����Բ��ֱ������ͼ2��ʾ����DEF�У���֪DE=DF����M��ֱ��EF�ϴ������˶�����M����E��F�غϣ�������M��ÿһ��λ�ã��ǡ�DEM�����Բ������DMF�����Բ����ı�ֵΪ�ˣ���ô��������
| A�� | ���ȱ�С�ٱ�� | |
| B�� | ����MΪ�߶�EF���е�ʱ����ȡ�����ֵ | |
| C�� | ���ȱ���ٱ�С | |
| D�� | ����һ����ֵ |
���� ���DEM�����Բ�뾶ΪR1����DMF�����Բ�뾶ΪR2���������⣬$\frac{{��R}_{1}^{2}}{��{R}_{2}^{2}}$=�ˣ������Ҷ����ɵã�R1=$\frac{1}{2}$$\frac{DE}{sin��DME}$��R2=$\frac{1}{2}$$\frac{DF}{sin��DMF}$�����DE=DF��sin��DME=sin��DMF���ɵæ�=1�����ɵý⣮
��� �⣺���DEM�����Բ�뾶ΪR1����DMF�����Բ�뾶ΪR2��
�������⣬$\frac{{��R}_{1}^{2}}{��{R}_{2}^{2}}$=�ˣ�
��M��ֱ��EF�ϴ������˶�����M����E��F�غϣ���
����M��ÿһ��λ�ã������Ҷ����ɵã�R1=$\frac{1}{2}$$\frac{DE}{sin��DME}$��R2=$\frac{1}{2}$$\frac{DF}{sin��DMF}$��
��DE=DF��sin��DME=sin��DMF��
�ɵã�R1=R2��
�ɵã���=1��
��ѡ��D��
���� ������Ҫ���������Ҷ����ڽ��������е�Ӧ�ã������˷�������˼���ת��˼���Ӧ�ã����ڻ����⣮

��ϰ��ϵ�д�
 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д�
�����Ŀ
12����֪����f��x��$\left\{\begin{array}{l}{{a}^{x}-2a��x��0}\\{-4ax+a��x��0}\end{array}\right.$������a��0����a��1����f��x����R�ϵ�������a��ȡֵ��Χ�ǣ�������
| A�� | ��0��$\frac{1}{3}$] | B�� | [$\frac{1}{3}$��1�� | C�� | ��0��$\frac{1}{2}$] | D�� | [$\frac{1}{2}$��1�� |
13����֪����ʵ��a��b����a��b�������в���ʽ��һ���������ǣ�������
| A�� | a+b��0 | B�� | $\frac{1}{a}��\frac{1}{b}$ | C�� | ab��b2 | D�� | a3-b3��0 |
14����$a={3^{0.2}}��b={log_��}3��c={log_3}cos\frac{{\sqrt{2}}}{4}��$����a��b��c��ϵ��ȷ���ǣ�������
| A�� | b��a��c | B�� | a��b��c | C�� | b��c��a | D�� | c��b��a |