题目内容
12．已知复数z满足（1-i）z=2i，其中i为虚数单位，则z的模为$\sqrt{2}$．分析 由（1-i）z=2i，得$z=\frac{2i}{1-i}$，然后利用复数代数形式的乘除运算化简复数z，再由复数求模公式计算得答案．
解答 解：由（1-i）z=2i，
得$z=\frac{2i}{1-i}$=$\frac{2i（1+i）}{（1-i）（1+i）}=-1+i$，
则z的模为：$\sqrt{（-1）^{2}+1}=\sqrt{2}$．
故答案为：$\sqrt{2}$．
点评 本题考查了复数代数形式的乘除运算，考查了复数模的求法，是基础题．
练习册系列答案
相关题目
2．在△ABC中，有正弦定理：$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$=定值，这个定值就是△ABC的外接圆的直径．如图2所示，△DEF中，已知DE=DF，点M在直线EF上从左到右运动（点M不与E、F重合），对于M的每一个位置，记△DEM的外接圆面积与△DMF的外接圆面积的比值为λ，那么（ ）
| A． | λ先变小再变大 | |
| B． | 仅当M为线段EF的中点时，λ取得最大值 | |
| C． | λ先变大再变小 | |
| D． | λ是一个定值 |
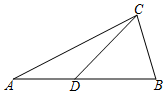如图所示，点D 在线段AB 上，∠CAD=30°，∠CDB=50°．给出下列三组条件（给出线段的长度）：