题目内容
14.设$a={3^{0.2}},b={log_π}3,c={log_3}cos\frac{{\sqrt{2}}}{4}π$,则a,b,c关系正确的是( )| A. | b>a>c | B. | a>b>c | C. | b>c>a | D. | c>b>a |
分析 利用指数函数、对数函数的单调性求解.
解答 解:∵$a={3^{0.2}},b={log_π}3,c={log_3}cos\frac{{\sqrt{2}}}{4}π$,
∴a=30.2>30=1,
0=logπ1<b=$lo{g}_{π}3,
$c=lo{g}_{3}cos\frac{\sqrt{2}}{4}π$<log31=0,
∴a,b,c关系为a>b>c.
故选:B.
点评 本题考查三个数的大小的求法,是基础题,解题时要认真审题,注意指数函数、对数函数的单调性的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.一个几何体的三视图如图所示,则该几何体的体积是( )
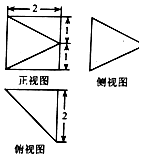

| A. | $\frac{8}{3}$ | B. | 4$\sqrt{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | 8 |
5.若命题:“$?{x_0}∈R,a{x^2}-ax-2>0$”为假命题,则a的取值范围是( )
| A. | (-∞,-8]∪[0,+∞) | B. | (-8,0) | C. | (-∞,0] | D. | [-8,0] |
2.在△ABC中,有正弦定理:$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$=定值,这个定值就是△ABC的外接圆的直径.如图2所示,△DEF中,已知DE=DF,点M在直线EF上从左到右运动(点M不与E、F重合),对于M的每一个位置,记△DEM的外接圆面积与△DMF的外接圆面积的比值为λ,那么( )

| A. | λ先变小再变大 | |
| B. | 仅当M为线段EF的中点时,λ取得最大值 | |
| C. | λ先变大再变小 | |
| D. | λ是一个定值 |
9.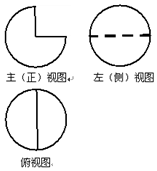 一个几何体的三视图如图所示,其中俯视图与左视图均为半径是1的圆,则这个几何体的体积是( )
一个几何体的三视图如图所示,其中俯视图与左视图均为半径是1的圆,则这个几何体的体积是( )
 一个几何体的三视图如图所示,其中俯视图与左视图均为半径是1的圆,则这个几何体的体积是( )
一个几何体的三视图如图所示,其中俯视图与左视图均为半径是1的圆,则这个几何体的体积是( )| A. | $\frac{4π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | π |
19.下列四个函数中,在其定义域上既是奇函数又是单调递增函数的是( )
| A. | y=ex | B. | y=sinx | C. | $y=\sqrt{x}$ | D. | y=x3 |