题目内容
11.如图1,四边形ABCD为正方形,延长DC至E,使得CE=2DC,将四边形ABCD沿BC折起到A1BCD1的位置,使平面A1BCD1⊥平面BCE,如图2.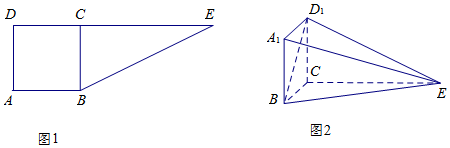
(I)求证:CE⊥平面A1BCD1;
(II)求异面直线BD1与A1E所成角的大小;
(III)求平面BCE与平面A1ED1所成锐二面角的余弦值.
分析 (Ⅰ)推导出CE⊥BC,CE⊥平面A1BCD1.
(Ⅱ)法一:连接A1C.推导出A1C⊥BD1,CE⊥BD1,从而BD1⊥A1E.由此能求出异面直线BD1与A1E所成的角.
法二:以C为坐标原点,建立空间直角坐标系,利用向量法能求出异面直线BD1与A1E所成的角.
(Ⅲ) 求出平面BCE的法向量和平面A1D1E的法向量,利用向量法能求出平面BCE与平面A1ED1所成的锐二面角的余弦值.
解答 (本小题满分14分)
证明:(Ⅰ)因为平面A1BCD1⊥平面BCE,且平面A1BCD1∩平面BCE=BC,
四边形ABCD为正方形,E在DC的延长线上,
所以CE⊥BC.
因为CE?平面BCE,
所以CE⊥平面A1BCD1.…(4分)
解:(Ⅱ)法一:连接A1C.因为A1BCD1是正方形,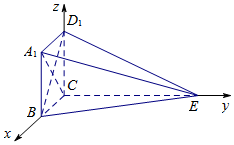 所以A1C⊥BD1.
所以A1C⊥BD1.
因为CE⊥平面A1BCD1,所以CE⊥BD1.
因为A1C∩CE=C,所以BD1⊥平面A1CE.
所以BD1⊥A1E.
所以异面直线BD1与A1E所成的角是90°.…(9分)
法二:以C为坐标原点,建立空间直角坐标系如图所示.
设CD=1,则CE=2.
则C(0,0,0),B(1,0,0),E(0,2,0),D1(0,0,1),A1(1,0,1).
所以${\overrightarrow{BD}_1}=(-1,0,1),\overrightarrow{{A_1}E}=(-1,2,-1)$.
因为$cos<\overrightarrow{B{D_1}},\overrightarrow{{A_1}E}>=\frac{{\overrightarrow{B{D_1}}•\overrightarrow{{A_1}E}}}{{|{\overrightarrow{B{D_1}}}||{\overrightarrow{{A_1}E}}|}}=\frac{1+0-1}{{\sqrt{2}×\sqrt{6}}}=0$,
所以$\overrightarrow{B{D_1}}⊥\overrightarrow{{A_1}E}$.
所以异面直线BD1与A1E所成的角是90°.…(9分)
(Ⅲ) 因为CD1⊥平面BCE,所以平面BCE的法向量$\overrightarrow{C{D_1}}=(0,0,1)$.
设平面A1D1E的法向量$\overrightarrow n=(x,y,z)$.
因为$\overrightarrow{{D_1}{A_1}}=(1,0,0),\overrightarrow{{D_1}E}=(0,2,-1)$,
所以$\left\{\begin{array}{l}\overrightarrow n•\overrightarrow{{D_1}{A_1}}=0\\ \overrightarrow n•\overrightarrow{{D_1}E}=0\end{array}\right.$,即$\left\{\begin{array}{l}x=0\\ 2y-z=0\end{array}\right.$.设y=1,则z=2.所以$\overrightarrow n=(0,1,2)$.
因为$cos<\overrightarrow{C{D_1}},\overrightarrow n>=\frac{{\overrightarrow{C{D_1}}•\overrightarrow n}}{{|{\overrightarrow{C{D_1}}}||{\overrightarrow n}|}}=\frac{0+0+2}{{\sqrt{5}}}=\frac{{2\sqrt{5}}}{5}$
所以平面BCE与平面A1ED1所成的锐二面角的余弦值为$\frac{{2\sqrt{5}}}{5}$.…(14分)
点评 本题考查线面垂直的证明,考查异面直线所成角的求法,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

| A. | 6 | B. | 8 | C. | 10 | D. | 12 |

| A. | λ先变小再变大 | |
| B. | 仅当M为线段EF的中点时,λ取得最大值 | |
| C. | λ先变大再变小 | |
| D. | λ是一个定值 |
| A. | y=ex | B. | y=sinx | C. | $y=\sqrt{x}$ | D. | y=x3 |
| A. | 4 | B. | -4 | C. | 2 | D. | -2 |
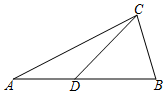 如图所示,点D 在线段AB 上,∠CAD=30°,∠CDB=50°.给出下列三组条件(给出线段的长度):
如图所示,点D 在线段AB 上,∠CAD=30°,∠CDB=50°.给出下列三组条件(给出线段的长度):