题目内容
12.已知函数f(x)$\left\{\begin{array}{l}{{a}^{x}-2a,x>0}\\{-4ax+a,x≤0}\end{array}\right.$,其中a>0,且a≠1,若f(x)在R上单调,则a的取值范围是( )| A. | (0,$\frac{1}{3}$] | B. | [$\frac{1}{3}$,1) | C. | (0,$\frac{1}{2}$] | D. | [$\frac{1}{2}$,1) |
分析 根据f(x)在R上单调,可知a<1,那么-4a<0,且满足(ax-2a)max≤(-4ax+a)min可得a的取值范围.
解答 解:函数f(x)$\left\{\begin{array}{l}{{a}^{x}-2a,x>0}\\{-4ax+a,x≤0}\end{array}\right.$,其中a>0,且a≠1,
f(x)在R上单调,观察选项,可知:y=ax-2a是减函数,则a<1.
∴y=-4ax+a也是减函数,则-4a<0,即a>0.
且满足(ax-2a)max≤(-4ax+a)min,可得:1-2a≤a,
解得:$a≥\frac{1}{3}$.
综上可得:a的取值范围是[$\frac{1}{3}$,1).
故选B.
点评 本题考查了分段函数的单调性的运用.属于基础题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
2.已知函数y=f(x)满足f(x+1)=x+3a,且f(a)=3.
(1)求函数f(x)的解析式;
(2)若g(x)=x•f(x)+λf(x)+1在(0,2)上具有单调性,λ<0,求g(λ)的取值范围.
(1)求函数f(x)的解析式;
(2)若g(x)=x•f(x)+λf(x)+1在(0,2)上具有单调性,λ<0,求g(λ)的取值范围.
20.已知O,A,B三地在同一水平面内,A地在O地正东方向2km处,B地在O地正北方向2km处,某测绘队员在A、B之间的直线公路上任选一点C作为测绘点,用测绘仪进行测绘,O地为一磁场,距离其不超过$\sqrt{3}km$的范围内对测绘仪等电子仪器形成干扰,使测量结果不准确,则该测绘队员能够得到准确数据的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $1-\frac{{\sqrt{3}}}{2}$ | D. | $1-\frac{{\sqrt{2}}}{2}$ |
7.设函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}x,x>0}\\{\frac{1}{1-x},x<0}\end{array}\right.$,则f(f(-3))等于( )
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
4.一个几何体的三视图如图所示,则该几何体的体积是( )
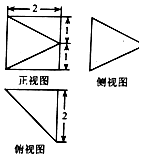

| A. | $\frac{8}{3}$ | B. | 4$\sqrt{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | 8 |
1.从0,1,2,3,4中任选两个不同的数字组成一个两位数,其中偶数的个数是( )
| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
2.在△ABC中,有正弦定理:$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$=定值,这个定值就是△ABC的外接圆的直径.如图2所示,△DEF中,已知DE=DF,点M在直线EF上从左到右运动(点M不与E、F重合),对于M的每一个位置,记△DEM的外接圆面积与△DMF的外接圆面积的比值为λ,那么( )

| A. | λ先变小再变大 | |
| B. | 仅当M为线段EF的中点时,λ取得最大值 | |
| C. | λ先变大再变小 | |
| D. | λ是一个定值 |
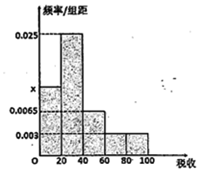 我市随机抽取部分企业调查年上缴税收情况(单位:万元),将所得数据绘制成频率分布直方图(如图),年上缴税收范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100]
我市随机抽取部分企业调查年上缴税收情况(单位:万元),将所得数据绘制成频率分布直方图(如图),年上缴税收范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100]