题目内容
13.已知非零实数a,b满足a<b,则下列不等式中一定成立的是( )| A. | a+b>0 | B. | $\frac{1}{a}>\frac{1}{b}$ | C. | ab<b2 | D. | a3-b3<0 |
分析 根据不等式的性质求解即可.
解答 解:对于A:∵a<b,则a-b<0,b-a>0,∴A不对.
对于B:∵a<b,当a<0<b,则$\frac{1}{a}<\frac{1}{b}$,∴B不对.
对于C:∵a<b,当a<b<0,则ab>b2,∴C不对.
对于D:∵a<b,则a3<b3,即a3-b3<0,∴D对.
故选D.
点评 本题考查了不等式的基本性质的运用.比较基础.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
4.一个几何体的三视图如图所示,则该几何体的体积是( )
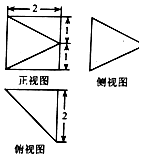

| A. | $\frac{8}{3}$ | B. | 4$\sqrt{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | 8 |
1.从0,1,2,3,4中任选两个不同的数字组成一个两位数,其中偶数的个数是( )
| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
5.若命题:“$?{x_0}∈R,a{x^2}-ax-2>0$”为假命题,则a的取值范围是( )
| A. | (-∞,-8]∪[0,+∞) | B. | (-8,0) | C. | (-∞,0] | D. | [-8,0] |
2.在△ABC中,有正弦定理:$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$=定值,这个定值就是△ABC的外接圆的直径.如图2所示,△DEF中,已知DE=DF,点M在直线EF上从左到右运动(点M不与E、F重合),对于M的每一个位置,记△DEM的外接圆面积与△DMF的外接圆面积的比值为λ,那么( )

| A. | λ先变小再变大 | |
| B. | 仅当M为线段EF的中点时,λ取得最大值 | |
| C. | λ先变大再变小 | |
| D. | λ是一个定值 |
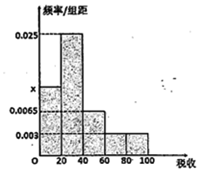 我市随机抽取部分企业调查年上缴税收情况(单位:万元),将所得数据绘制成频率分布直方图(如图),年上缴税收范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100]
我市随机抽取部分企业调查年上缴税收情况(单位:万元),将所得数据绘制成频率分布直方图(如图),年上缴税收范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100]