题目内容
已知函数f(x)=ax2+x-xlnx(a>0).
(1)已知直线y=x+1与g(x)=f′(x)相切,求a的值;
(2)若函数满足f(1)=2,且在定义域内f(x)>bx2+2x恒成立,求实数b的取值范围;
(3)若函数f(x)在定义域上是单调函数,求实数a的取值范围.
(1)已知直线y=x+1与g(x)=f′(x)相切,求a的值;
(2)若函数满足f(1)=2,且在定义域内f(x)>bx2+2x恒成立,求实数b的取值范围;
(3)若函数f(x)在定义域上是单调函数,求实数a的取值范围.
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:函数的性质及应用,导数的综合应用
分析:(1)f′(x)=2ax-lnx,(x>0),故g(x)=2ax-lnx,(x>0),g′(x)=2a-
,设切点为(t,g(t)),由斜率k=g′(t)=2a-
=1,及g(t)=t+1,
联立方程可解得a.
(2)依题意x2+x-xlnx)≥bx2+2x恒成立?1-
-
≥b,构造函数g(x)=1-
-
,利用导数可求得g(x)min,从而可求得实数b的取值范围;
(3)f′(x)=2ax-lnx,(x>0),令f′(x)≥0可求得a的范围,对a的范围分情况讨论可由f(x)在定义域上是单调函数,求得实数a的取值范围;
| 1 |
| x |
| 1 |
| t |
联立方程可解得a.
(2)依题意x2+x-xlnx)≥bx2+2x恒成立?1-
| 1 |
| x |
| lnx |
| x |
| 1 |
| x |
| lnx |
| x |
(3)f′(x)=2ax-lnx,(x>0),令f′(x)≥0可求得a的范围,对a的范围分情况讨论可由f(x)在定义域上是单调函数,求得实数a的取值范围;
解答:
解:(1)f′(x)=2ax-lnx,(x>0),故g(x)=2ax-lnx,(x>0),
g′(x)=2a-
,设切点为(t,g(t)),∴斜率k=g′(t)=2a-
=1,∵g(t)=t+1,∴2at-lnt=t+1,∴
,
解得t=1,a=1.
(2)由f(1)=2,得a=1,又x>0,
∴x2+x-xlnx)≥bx2+2x恒成立?1-
-
≥b,
令g(x)=1-
-
,∴g′(x)=
,可得g(x)在(0,1]上递减,
在[1,+∞)上递增,所以g(x)min=g(1)=0,
即b≤0.
(3)f′(x)=2ax-lnx,(x>0),
令f′(x)≥0得:2a≥
,设h(x)=
,∴h′(x)=
,
当x=e时,h(x)max=
,
∴当a≥
时,函数f(x)在(0,+∞)单调递增,
若0<a<
,g(x)=2ax-lnx,(x>0),g′(x)=2a-
,
g′(x)=0,x=
,x∈(0,
),g′(x)<0,x∈(
,+∞),g′(x)>0,
∴x=
时取得极小值,即最小值.
而当0<a<
时,g(
)=1-ln
<0,
f′(x)=0必有根,f(x)必有极值,在定义域上不单调,
∴a≥
.
g′(x)=2a-
| 1 |
| x |
| 1 |
| t |
|
解得t=1,a=1.
(2)由f(1)=2,得a=1,又x>0,
∴x2+x-xlnx)≥bx2+2x恒成立?1-
| 1 |
| x |
| lnx |
| x |
令g(x)=1-
| 1 |
| x |
| lnx |
| x |
| lnx |
| x2 |
在[1,+∞)上递增,所以g(x)min=g(1)=0,
即b≤0.
(3)f′(x)=2ax-lnx,(x>0),
令f′(x)≥0得:2a≥
| lnx |
| x |
| lnx |
| x |
| 1-lnx |
| x2 |
当x=e时,h(x)max=
| 1 |
| e |
∴当a≥
| 1 |
| 2e |
若0<a<
| 1 |
| 2e |
| 1 |
| x |
g′(x)=0,x=
| 1 |
| 2a |
| 1 |
| 2a |
| 1 |
| 2a |
∴x=
| 1 |
| 2a |
而当0<a<
| 1 |
| 2e |
| 1 |
| 2a |
| 1 |
| 2a |
f′(x)=0必有根,f(x)必有极值,在定义域上不单调,
∴a≥
| 1 |
| 2e |
点评:此题考查函数单调性与导数的关系的应用,考查学生会利用导函数的正负确定函数的单调区间,掌握函数恒成立时所取的条件,是一道综合题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
8788+7除以88的余数是( )
| A、0 | B、1 | C、8 | D、80 |
△ABC中,BC=2,A=45°,B为锐角,点O是△ABC外接圆的圆心,则
•
的取值范围是( )
| OA |
| BC |
A、(-2,2
| ||||
B、(-2
| ||||
C、[-2
| ||||
| D、(-2,2) |
下列说法不正确的是( )
| A、命题“对?x∈R,都有x2≥0”的否定为“?x0∈R,使得x02<0” | ||||
| B、“a>b”是“ac2>bc2”的必要不充分条件 | ||||
C、“若tanα≠
| ||||
| D、甲、乙两位学生参与数学模拟考试,设命题p是“甲考试及格”,q是“乙考试及格”,则命题“至少有一位学生不及格”可表示为(¬p)∧(¬q) |
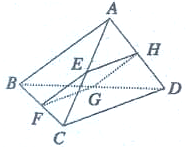 如图四边形EFGH为空间四面体A-BCD的一个截面,若截面为平行四边形.
如图四边形EFGH为空间四面体A-BCD的一个截面,若截面为平行四边形.