题目内容
△ABC中,BC=2,A=45°,B为锐角,点O是△ABC外接圆的圆心,则
•
的取值范围是( )
| OA |
| BC |
A、(-2,2
| ||||
B、(-2
| ||||
C、[-2
| ||||
| D、(-2,2) |
考点:平面向量数量积的运算
专题:三角函数的求值,三角函数的图像与性质,平面向量及应用
分析:首先建立恰当的直角坐标系,根据直角坐标系确定各点的坐标,进一步利用向量的数量积转化成利用定义域求三角函数的值域.最后求的结果.
解答:
解:如图所示:|BC|=2,∠BOC=90°,∠CAB=45°,
由于∠B为锐角,则:点A只能在左半圆上,
故设:A(
cosθ,
sinθ)(
<θ<
)
B(
,0),C(0,
)
所以:
=(
cosθ,
sinθ),
=(-
,
)
•
=-2cosθ+2sinθ=2
sin(θ-
)
由于
<θ<
所以:-
<sin(θ-
)≤1
则:-2<
•
≤2
故选:A
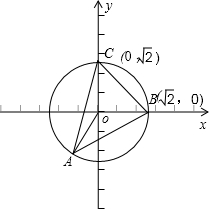
由于∠B为锐角,则:点A只能在左半圆上,
故设:A(
| 2 |
| 2 |
| π |
| 2 |
| 3π |
| 2 |
B(
| 2 |
| 2 |
所以:
| OA |
| 2 |
| 2 |
| BC |
| 2 |
| 2 |
| OA |
| BC |
| 2 |
| π |
| 4 |
由于
| π |
| 2 |
| 3π |
| 2 |
所以:-
| ||
| 2 |
| π |
| 4 |
则:-2<
| OA |
| BC |
| 2 |
故选:A

点评:本题考查的知识要点:向量的数量积,三角函数的恒等变换,利用正弦型函数的定义域求值域.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
已知全集U={0,1,2,4,6,8,10},集合A={2,4,6},B={1},则∁UA∪B等于( )
| A、{0,1,8,10} |
| B、{1,2,4,6} |
| C、{0,8,10} |
| D、Φ |