题目内容
设α，β是两个平面，α∩β=b，且直线a∥α，a∥β，那么请画图表示a与b的位置关系．并证明．
考点：空间中直线与直线之间的位置关系
专题：证明题,空间位置关系与距离
分析：过a作两个平面M，N，使得M∩β=c，N∩α=d，由线面平行的性质定理得，a∥c，a∥d，则c∥d，再由线面平行的判定定理得，c∥α，再由线面平行的性质定理，可得c∥b，再由公理4，即可得到a∥b．
解答：
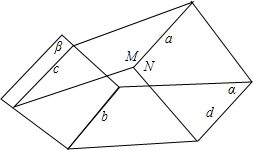解：a与b的位置关系：平行．
理由如下：由于直线a∥α，a∥β，
过a作两个平面M，N，使得M∩β=c，N∩α=d，
由线面平行的性质定理得，a∥c，a∥d，
则c∥d，
c?α，d?α，则c∥α，
又α∩β=b，
即有c∥b，
又c∥a，
故a∥b．
解：a与b的位置关系：平行．理由如下：由于直线a∥α，a∥β，
过a作两个平面M，N，使得M∩β=c，N∩α=d，
由线面平行的性质定理得，a∥c，a∥d，
则c∥d，
c?α，d?α，则c∥α，
又α∩β=b，
即有c∥b，
又c∥a，
故a∥b．
点评：本题考查线面平行的判定定理和性质定理的运用，两直线位置关系的判断，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
2sin22.5°cos22.5°=（ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
已知全集U={0，1，2，4，6，8，10}，集合A={2，4，6}，B={1}，则∁UA∪B等于（ ）
| A、{0，1，8，10} |
| B、{1，2，4，6} |
| C、{0，8，10} |
| D、Φ |
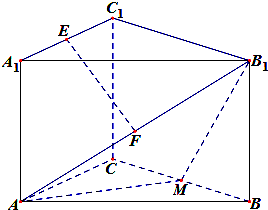在正三棱柱ABC-A1B1C1中，BC=