题目内容
已知数列{an}的前五项是一个以-2为首项,以3为公差的等差数列,从第五项起数列{an}成等比数列,若Sn为数列{an}的前n项和,且
Sn=40,求
(1)数列{an}的通项公式
(2)数列{an}的前n项和Sn的表达式.
| lim |
| n→∞ |
(1)数列{an}的通项公式
(2)数列{an}的前n项和Sn的表达式.
考点:数列的极限,数列的求和
专题:等差数列与等比数列
分析:(1)由已知结合数列极限求得等比数列的公比,然后分段写出等比数列的通项公式;
(2)分数列为等差数列和等比数列两段分段写出数列{an}的前n项和Sn的表达式.
(2)分数列为等差数列和等比数列两段分段写出数列{an}的前n项和Sn的表达式.
解答:
解:(1)由题意知,S4=4×(-2)+
=10,a5=-2+(5-1)×3=10.
则Sn=S4+a5+a6+…+an=10+
.
由
Sn=40,得
[10+
]=10+
=40,
∴
=30,解得q=
.
则当n≤5时,an=-2+3(n-1)=3n-5;
当n>5时,an=10•(
)n-5.
故an=
;
(2)当n≤5时,Sn=-2n+
×3=
n2-
n;
当n>5时,Sn=20+
=40-20•(
)n-5.
故Sn=
.
| 4×3×3 |
| 2 |
则Sn=S4+a5+a6+…+an=10+
| 10(1-qn-4) |
| 1-q |
由
| lim |
| n→∞ |
| lim |
| n→∞ |
| 10(1-qn-4) |
| 1-q |
| lim |
| n→∞ |
| 10(1-qn-4) |
| 1-q |
∴
| 10 |
| 1-q |
| 2 |
| 3 |
则当n≤5时,an=-2+3(n-1)=3n-5;
当n>5时,an=10•(
| 2 |
| 3 |
故an=
|
(2)当n≤5时,Sn=-2n+
| n(n-1) |
| 2 |
| 3 |
| 2 |
| 7 |
| 2 |
当n>5时,Sn=20+
10×
| ||||
1-
|
| 2 |
| 3 |
故Sn=
|
点评:本题考查了数列极限,考查了等差数列和等比数列的通项公式,考查了等差数列和等比数列的前n项和,是中档题.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
下列选项叙述错误的是( )
| A、命题“若x≠0,则ex≠1”的逆否命题是“若ex=1,则x=0” | ||
B、“x>2”是“
| ||
| C、若命题p:?x∈R,x2+x+1>0,则¬p:?x0∈R,使得x02+x0+1≤0 | ||
| D、若p∧q为假命题,则p,q均为假命题 |
直线l:y=kx-1与曲线C:x2+y2-4x+3=0有且仅有2个公共点,则实数k的取值范围是( )
A、(0,
| ||||
B、(0,
| ||||
C、{
| ||||
D、{
|
已知函数f(x)=ex,对于曲线y=f(x)上横坐标城等差数列的三个点A、B、C,给出以下四个判断:①△ABC一定是钝角三角形;②△ABC可能是直角三角形;③△ABC可能是等腰三角形;④△ABC不可能是等腰三角形.其中正确的判断是( )
| A、①③ | B、①④ | C、②③ | D、②④ |
过点(2,2)引椭圆x2+4y2=4的切线,则切线方程为( )
| A、3x-8y+10=0 |
| B、5x+8y-2=0 |
| C、3x-8y+10=0或x-2=0 |
| D、5x+8y-2=0或3x+10=0 |
设x,y满足
,则z=x+y的最小值为( )
|
| A、-2 | B、-1 | C、1 | D、2 |
 如图,已知AB是⊙O的直径,CD是⊙O的切线,C为切点,AD⊥CD交⊙O于点E,连接AC、BC、OC、CE,延长AB交CD于F.
如图,已知AB是⊙O的直径,CD是⊙O的切线,C为切点,AD⊥CD交⊙O于点E,连接AC、BC、OC、CE,延长AB交CD于F.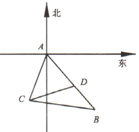 如图,某观测站C在A城的南偏西20°,一条笔直公路AB,其中B在A城南偏东40°,B与C相距31千米.有一人从B出发沿公路向A城走去,走了20千米后到达D处,此时C,D之间的距离为21千米,则A,C之间的距离是
如图,某观测站C在A城的南偏西20°,一条笔直公路AB,其中B在A城南偏东40°,B与C相距31千米.有一人从B出发沿公路向A城走去,走了20千米后到达D处,此时C,D之间的距离为21千米,则A,C之间的距离是