题目内容
若不等式x2+px+q>0的解集是{x|x>
或x<-
},则
= .
| 7 |
| 2 |
| 1 |
| 2 |
| p |
| q |
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:不等式x2+px+q>0的解集是{x|x>
或x<-
},可知:
,-
是一元二次方程x2+px+q=0的两个实数根,利用一元二次方程的根与系数的关系即可得出.
| 7 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
| 1 |
| 2 |
解答:
解:∵不等式x2+px+q>0的解集是{x|x>
或x<-
},
∴
,-
是一元二次方程x2+px+q=0的两个实数根,
∴-
+
=-p,-
×
=q,
∴
=
.
故答案为:
| 7 |
| 2 |
| 1 |
| 2 |
∴
| 7 |
| 2 |
| 1 |
| 2 |
∴-
| 1 |
| 2 |
| 7 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
∴
| p |
| q |
| 12 |
| 7 |
故答案为:
| 12 |
| 7 |
点评:本题考查了一元二次不等式的解集与相应的一元二次方程的实数及其根与系数的关系,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若sinαtanα>0,且sinαcosα<0,则α是( )
| A、第一象限角 |
| B、第二象限角 |
| C、第三象限角 |
| D、第四象限角 |
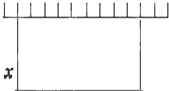 某工厂需要建一个面积为512m2的矩形堆料场,一边可以利用原有的墙壁,为了使砌墙所用的材料最省,则图中的x=
某工厂需要建一个面积为512m2的矩形堆料场,一边可以利用原有的墙壁,为了使砌墙所用的材料最省,则图中的x=