题目内容

抛物线y=
x2
4
的准线方程是
 
．
考点：抛物线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：先根据抛物线方程的标准形式，再根据抛物线的性质求出其准线方程即可．
解答： 解：抛物线的方程为x2=4y
故p=2
其准线方程为 y=-1
故答案为：y=-1．
点评：本题考查抛物线的简单性质，解题关键是记准抛物线的标准方程，别误认为p=-4，因看错方程形式马虎导致错误．
练习册系列答案
相关题目
已知（2，1）是直线l被椭圆
x2
16
+
y2
4
=1所截得的线段的中点，则直线l的方程是（　　）
A、x+2y-4=0
B、x-2y=0
C、x+8y-10=0
D、x-8y+6=0
已知f（x）对任意的实数m，n都有：f（m+n）=f（m）+f（n）-1，且当x＞0时，有f（x）＞1．
（1）求f（0）；
（2）求证：f（x）在R上为增函数；
（3）若f（6）=7，且关于x的不等式f（ax-2）+f（x-x2）＜3对任意的x∈[-1，+∞）恒成立，求实数a的取值范围．
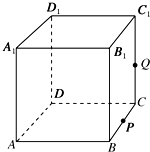如图正方体ABCD-A1B1C1D1，棱长为1，P为BC中点，Q为线段CC1上的动点，过A、P、Q的平面截该正方体所得的截面记为S，则下列命题正确的是
 
．（写出所有正确命题的编号） 
①当0＜CQ＜
1
2
时，S为四边形
②当CQ=
1
2
时，S为等腰梯形
③当CQ=
3
4
时，S与C1D1交点R满足C1R1=
1
3

④当
3
4
＜CQ＜1时，S为六边形
⑤当CQ=1时，S的面积为
6
．
已知函数f （x）=ax-ln x（a∈R）．
（Ⅰ）求f （x）的单调区间；
（Ⅱ）当a＞0时，求f （x）在区间（0，e]上的最小值．
已知抛物线的准线为x=-
P
2
（p＞0），顶点在原点，直线l：y=x-1过抛物线的焦点，并与抛物线交于A，B两点．求抛物线方程和弦长|AB|．
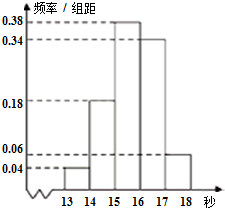高二某班50名学生在一次百米测试中，成绩全部都介于13秒到18秒之间，将测试结果按如下方式分成五组，第一组[13，14），第二组[14，15），…，第五组[17，18]，如图是按上述分组方法得到的频率分布直方图．
（1）若成绩在区间[14，16）内规定为良好，求该班在这次百米测试中成绩为良好的人数；
（2）请根据频率分布直方图估计样本数据的众数和中位数（精确到0.01）．
函数y=lg（sinx-cosx-1）的定义域为
 
．
已知圆O：x2+y2=4，过点M（1，
2
）的两条弦AC，BD互相垂直，则AC+BD的最大值是（　　）
A、6
B、2
10
C、4
3
D、5
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网