题目内容
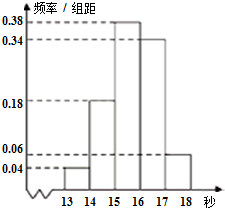 高二某班50名学生在一次百米测试中,成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
高二某班50名学生在一次百米测试中,成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.(1)若成绩在区间[14,16)内规定为良好,求该班在这次百米测试中成绩为良好的人数;
(2)请根据频率分布直方图估计样本数据的众数和中位数(精确到0.01).
考点:众数、中位数、平均数,频率分布直方图
专题:概率与统计
分析:(1)根据频率分布直方图,求出成绩在[14,16)内的频数;
(2)由频率分布直方图,得出众数是什么,求出中位数的值.
(2)由频率分布直方图,得出众数是什么,求出中位数的值.
解答:
解:(1)根据频率分布直方图知,
成绩在[14,16)内的人数为:50×0.18+50×0.38=28人;
(2)由频率分布直方图知,
众数落在第三组[15,16)内,是
=15.5;
∵数据落在第一、二组的频率为1×0.04+1×0.08=0.22<0.5,
数据落在第一、二、三组的频率为1×0.04+1×0.08+1×0.38=0.6>0.5,
∴中位数一定落在第三组[15,16)中;
设中位数是x,∴0.22+(x-15)×0.38=0.5,
解得中位数x=
≈15.7368≈15.74.
成绩在[14,16)内的人数为:50×0.18+50×0.38=28人;
(2)由频率分布直方图知,
众数落在第三组[15,16)内,是
| 15+16 |
| 2 |
∵数据落在第一、二组的频率为1×0.04+1×0.08=0.22<0.5,
数据落在第一、二、三组的频率为1×0.04+1×0.08+1×0.38=0.6>0.5,
∴中位数一定落在第三组[15,16)中;
设中位数是x,∴0.22+(x-15)×0.38=0.5,
解得中位数x=
| 299 |
| 19 |
点评:本题考查了频率分布直方图的应用问题,解题时应根据图中数据,会求中位数与众数,是基础题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
将函数y=sinx的图象向左平移
个单位,得到函数 y=sin(x+ϕ)(|ϕ|<
)的图象,则ϕ等于( )
| π |
| 12 |
| π |
| 2 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
已知等比数列{an}的前n项和为Sn=2•3n-2+m,则实数m的值为( )
| A、-2 | ||
B、-
| ||
C、
| ||
D、-
|