Question

已知圆O：x²+y²=4，过点M（1，

2

）的两条弦AC，BD互相垂直，则AC+BD的最大值是（　　）

• A、6
• B、2

  10

• C、4

  3

• D、5

  2

Answer 1

考点：圆的标准方程

专题：直线与圆

分析：作OE⊥AC、OF⊥BD，分别连接OB、OM、OC，则OE²=OC²-CE²，OF²=ME²=OM²-OE²=OM²-（OC²-CE²）=OM²+CE²-OC²，BF²=OB²-OF²=OB²-（OM²+CE²-OC²）=OB²+OC²-OM²-CE²=2（OB）²-OM²-CE²．由此能求出AC+BD的最大值．

解答： 解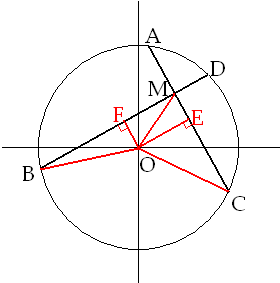：如图，作OE⊥AC、OF⊥BD，
分别连接OB、OM、OC，
则OE²=OC²-CE²，
OF²=ME²=OM²-OE²=OM²-（OC²-CE²）=OM²+CE²-OC²，
BF²=OB²-OF²=OB²-（OM²+CE²-OC²）
=OB²+OC²-OM²-CE²=2（OB）²-OM²-CE²．
由题意知：OB=2、OM=

3

，
故BF=

5-CE2

．
则：AC+BD=2CE+2BF=2（CE+BF）
=2（CE+

5-CE2

）
由不等式x+y≤

2(x2+y2)

，
得：CE+

5-CE2

≤

2

（CE²+5-CE²）=

10

．
所以AC+BD≤2

10

，即AC+BD的最大值为2

10

．
故答案为：2

10

．

点评：本题考查两条线段和的最大值的求法，解题时要认真审题，注意圆的性质的合理运用．