题目内容
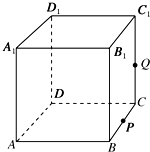 如图正方体ABCD-A1B1C1D1,棱长为1,P为BC中点,Q为线段CC1上的动点,过A、P、Q的平面截该正方体所得的截面记为S,则下列命题正确的是
如图正方体ABCD-A1B1C1D1,棱长为1,P为BC中点,Q为线段CC1上的动点,过A、P、Q的平面截该正方体所得的截面记为S,则下列命题正确的是①当0<CQ<
| 1 |
| 2 |
②当CQ=
| 1 |
| 2 |
③当CQ=
| 3 |
| 4 |
| 1 |
| 3 |
④当
| 3 |
| 4 |
⑤当CQ=1时,S的面积为
| 6 |
考点:棱柱的结构特征
专题:空间位置关系与距离
分析:易知,过点A,P,Q的平面必与面ADA1,BC1C相交,且交线平行,据此,当Q为C1C中点时,截面与面ADD1交与AD1,为等腰梯形,据此可以对①②进行判断;
连接AP,延长交DC于一点M,再连接MQ并延长其交D1D于N,连接AN,可见,截面此时不会与面ABB1相交,据此判断③④,
当CQ=1时,截面为底为
,腰长为
的等腰梯形,由此可求其面积.判断⑤.
连接AP,延长交DC于一点M,再连接MQ并延长其交D1D于N,连接AN,可见,截面此时不会与面ABB1相交,据此判断③④,
当CQ=1时,截面为底为
| 2 |
| ||
| 2 |
解答:
解:设截面与DD1相交于T,则AT∥PQ,且AT=2PQ⇒DT=2CQ.
对于①,当0<CQ<
时,则0<DT<1,所以截面S为四边形,且S为梯形,所以为真.
对于②,当CQ=
时,DT=1,T与D重合,截面S为四边形APQO1,所以AP=D1Q,截面为等腰梯形,所以为真.
对于③,当CQ=
,QC1=
,DT=2,D1T=
,利用三角形相似解得,C1R1=
,所以为真.
对于④,当
<CQ<1时,
<DT<2,截面S与线段A1D1,D1C1相交,所以四边形S为五边形,所以为假.
对于⑤,当CQ=1时,Q与C1重合,截面S与线段A1D1相交于中点G,即即为菱形APC1G,对角线长度为
和
,S的面积为
,所以为假,
综上,选①②③.
对于①,当0<CQ<
| 1 |
| 2 |
对于②,当CQ=
| 1 |
| 2 |
对于③,当CQ=
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
对于④,当
| 3 |
| 4 |
| 3 |
| 2 |
对于⑤,当CQ=1时,Q与C1重合,截面S与线段A1D1相交于中点G,即即为菱形APC1G,对角线长度为
| 2 |
| 3 |
| ||
| 2 |
综上,选①②③.
点评:此题考查了截面的性质,关键是利用面面平行、面面相交的性质确定截面的顶点.

练习册系列答案
相关题目
已知函数f(x)=
sinωx+cosωx(ω>0),y=f(x)的图象与直线y=2的两个相邻交点的距离等于π,则f(x)的一条对称轴是( )
| 3 |
A、x=-
| ||
B、x=
| ||
C、x=-
| ||
D、x=
|