题目内容
正四棱锥的底面面积为4,侧面积为5,则它的体积为 .
考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:利用正四棱锥的底面面积为4,求得底面正方形的边长,再根据侧面积为5求得斜高,利用斜高求得棱锥的高,代入棱锥的体积公式计算.
解答:
解:∵正四棱锥的底面面积为4,∴正四棱锥的底面正方形的边长为2,
设斜高为H,高为h,
则侧面积S=4×
×H×2=4H=5,∴H=
,
∴h=
=
,
∴几何体的体积V=
×2×2×
=1.
故答案为:1.
设斜高为H,高为h,
则侧面积S=4×
| 1 |
| 2 |
| 5 |
| 4 |
∴h=
| H2-12 |
| 3 |
| 4 |
∴几何体的体积V=
| 1 |
| 3 |
| 3 |
| 4 |
故答案为:1.
点评:本题考查了正棱锥的几何特征及棱锥的侧面积公式与体积公式,数列掌握正棱锥的性质是关键.

练习册系列答案
相关题目
 某几何体的三视图如图所示,其侧视图是一个边长为1的等边三角形,俯视图是两个正三角形拼成,则该几何体的体积为( )
某几何体的三视图如图所示,其侧视图是一个边长为1的等边三角形,俯视图是两个正三角形拼成,则该几何体的体积为( )| A、1 | ||
B、
| ||
C、
| ||
D、
|
命题“存在x∈R,使得x2+sinx-1≥0”的否定为( )
| A、对任意的x∈R,x2+sinx-1≥0 |
| B、不存在x∈R,使得x2+sinx-1≤0 |
| C、存在x∈R,使得x2+sinx-1<0 |
| D、对任意的x∈R,使得x2+sinx-1<0 |
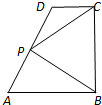 如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设